シミュレーティングで学ぶ アナログ&ディジタルフィルタ入門 小野浩司著 日本工業新聞社

ここで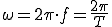 [rad/s]
[rad/s]
つまり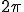 のとき1ラジアンとなる。
のとき1ラジアンとなる。
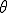 [rad]は位相である。
[rad]は位相である。
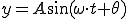
■例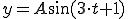
これだと、周波数も周期も分からない。
表記を簡単に示すときだけに使われる。
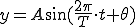
■例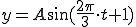
周期が3[s]であることが分かる。
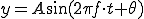
■例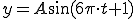
周波数が3[Hz]であることが分かる。
echo off
clear all
close all
%正弦波の周波数 5Hz
f=5
%正弦波の周期 0.2s
T = 1/f
%サンプリング周波数250Hz サンプル周期0.004s
dt=1/250
%周期は50点
num = T / dt
n=[0:1:2*num];
%信号波
omega=2*pi*f;
y=sin(omega*(n*dt));
plot(n,y,'r-','linewidth',2);
axis([-Inf Inf -Inf Inf]);
h=gca
set(h,'LineWidth',2,...,
'FontSize',15)
xlabel('Time','Fontsize',15);
ylabel('Amplitude','Fontsize',15)
title('Sin Wave');
print -djpeg sinwave.jpg
時間軸方向への移動を時間推移と呼ぶ。
いま、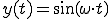
があると、
この正弦波波形を時間軸右方向へ![T_{shift} [s] T_{shift} [s]](B0CCC1EAA4C8BBFEB4D6BFE4B0DC_eq0012.gif) だけ平行移動した式は、
だけ平行移動した式は、
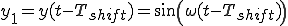
右へ平行移動: 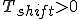
この場合、![T_{shift} = 0.5[ms] T_{shift} = 0.5[ms]](B0CCC1EAA4C8BBFEB4D6BFE4B0DC_eq0015.gif) では、
では、
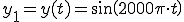
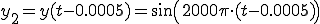
となり、 は、
は、 に対して右へ平行移動している。
に対して右へ平行移動している。
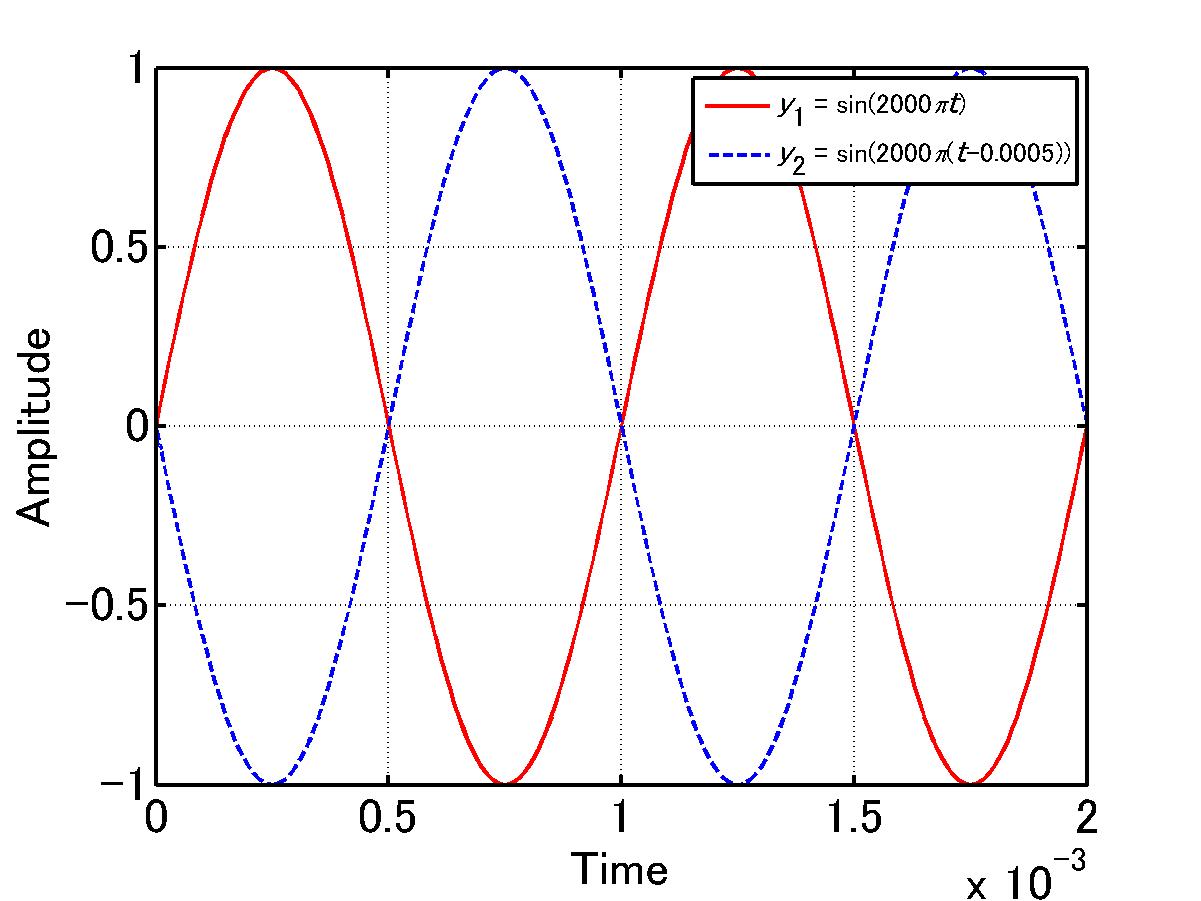
 は、0.0005秒後に
は、0.0005秒後に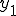 の0秒時と同じになるので
の0秒時と同じになるので
0.0005秒遅れているとも言える。
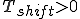 右へ平行移動: 遅れている
右へ平行移動: 遅れている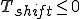 左へ平行移動: 進んでいる
左へ平行移動: 進んでいる
とも言える。
echo off
clear all
close all
dt=0.00001
num = 100
n=[0:1:2*num];
nn= dt.*n;
omega=2000*pi;
y1=sin(omega*(n*dt));
plot(nn,y1,'r-','linewidth',2);
axis([-Inf Inf -Inf Inf]);
grid on
hold on
y2=sin(omega*(n*dt-0.0005));
plot(nn,y2,'b--','linewidth',2);
axis([-Inf Inf -Inf Inf]);
h=legend('\it{y}\rm_1 = sin(2000\it{\pit}\rm)',...,
'\it{y}\rm_2 = sin(2000\it{\pi}\rm(\it{t}\rm-0.0005))',...,
1);
set(h,'FontSize',13);
h=gca
set(h,'LineWidth',2,...,
'FontSize',18)
xlabel('Time','Fontsize',18);
ylabel('Amplitude','Fontsize',18)
print -djpeg sinwave_zikansuii.jpg
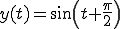 ここで、
ここで、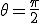
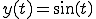 ここで、
ここで、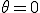
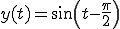 ここで、
ここで、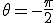
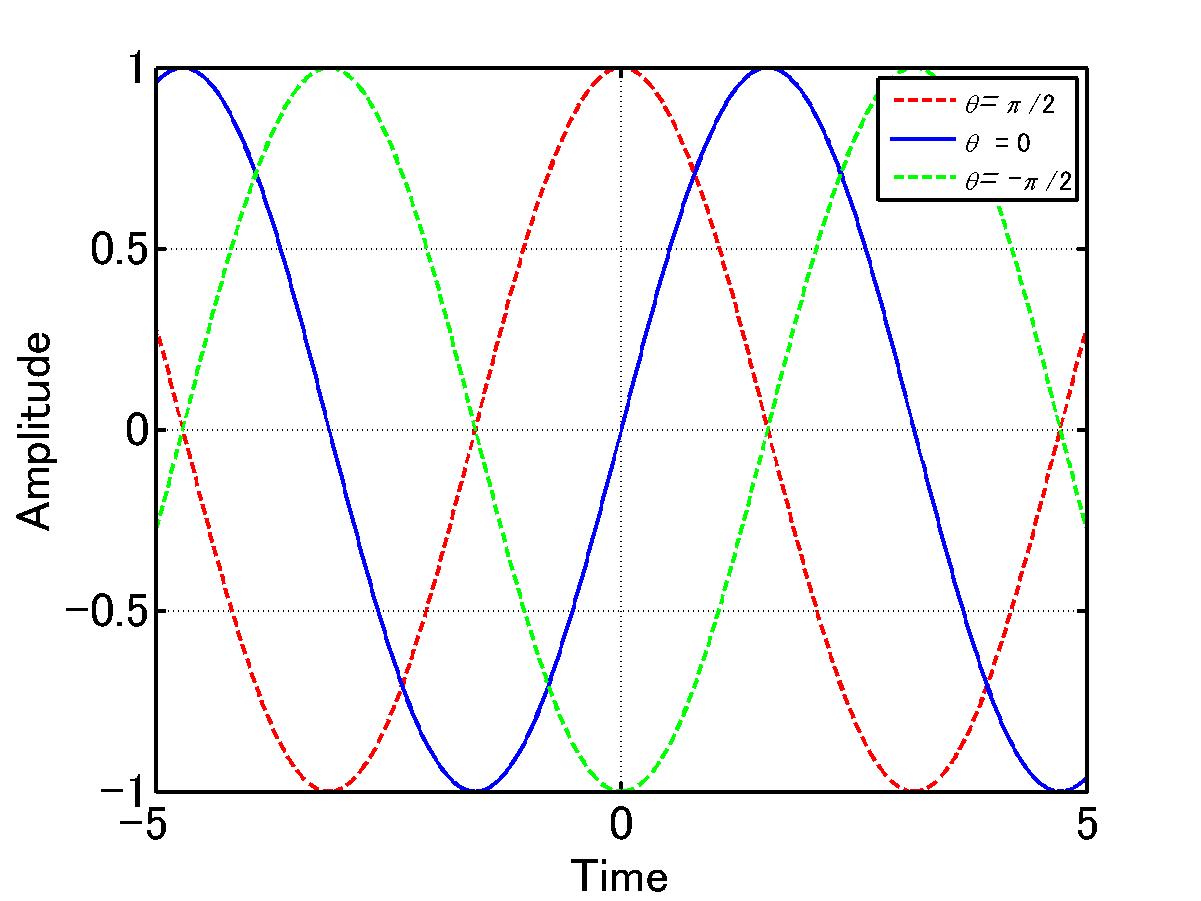
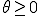 のときは、正弦波は左にずれる、これを位相進み(進み位相)と呼ぶ。
のときは、正弦波は左にずれる、これを位相進み(進み位相)と呼ぶ。
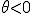 のtきは、正弦波は右にずれる、これを位相遅れ(遅れ位相)と呼ぶ。
のtきは、正弦波は右にずれる、これを位相遅れ(遅れ位相)と呼ぶ。
echo off
clear all
close all
dt=0.01
num = 250
n=[-2*num:1:2*num];
nn= dt.*n;
theta1= pi/2;
y1=sin((n*dt)+theta1);
plot(nn,y1,'r--','linewidth',2);
axis([-Inf Inf -Inf Inf]);
grid on
hold on
theta2= 0;
y2=sin((n*dt)+theta2);
plot(nn,y2,'b-','linewidth',2);
axis([-Inf Inf -Inf Inf]);
grid on
hold on
theta3= -pi/2;
y3=sin((n*dt)+theta3);
plot(nn,y3,'g--','linewidth',2);
axis([-Inf Inf -Inf Inf]);
h=legend('\it{\theta}= \pi \rm/2',...,
'\it{\theta} \rm = 0',...,
'\it{\theta}= -\pi \rm/2',...,
1);
set(h,'FontSize',13);
h=gca
set(h,'LineWidth',2,...,
'FontSize',18)
xlabel('Time','Fontsize',18);
ylabel('Amplitude','Fontsize',18)
print -djpeg sinwave_isou.jpg
正弦波が左へずれる: 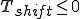 ,
, 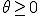 (位相進み)
(位相進み)
正弦波が右へずれる: 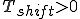
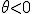 (位相遅れ)
(位相遅れ)
位相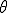 と
と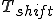 の符号が逆になっていることに注意!
の符号が逆になっていることに注意!
理由は以下のとおり!
今 正弦波を、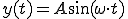
とすると、
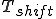 だけ右へずらした波形は、
だけ右へずらした波形は、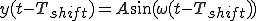
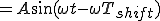
ゆえに、
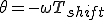
これは、マイナスの符号がついているため位相遅れとなる。
この式から、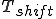 と
と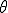 の符号が反対なのが分かる。
の符号が反対なのが分かる。