Matlabでは
fft
という命令だけでFFTしてくれるが使い方に注意!
以下にサンプルで示す。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Matlab FFT sample program
% programming by embedded.samurai
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
echo off
clear all
close all
%サンプリング周期 50[ms]
dt=50e-3;
%サンプリング周波数20Hz 10Hz以下まで表すことができる
df=1/dt;
%離散時間(横軸)を作る
t=[0:dt:50];
%50msごとの離散時間が何個で構成されるか調べる
[gyo retu]=size(t)
%gyo行、retu列の0データを作る。
zerodata = zeros(gyo,retu);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
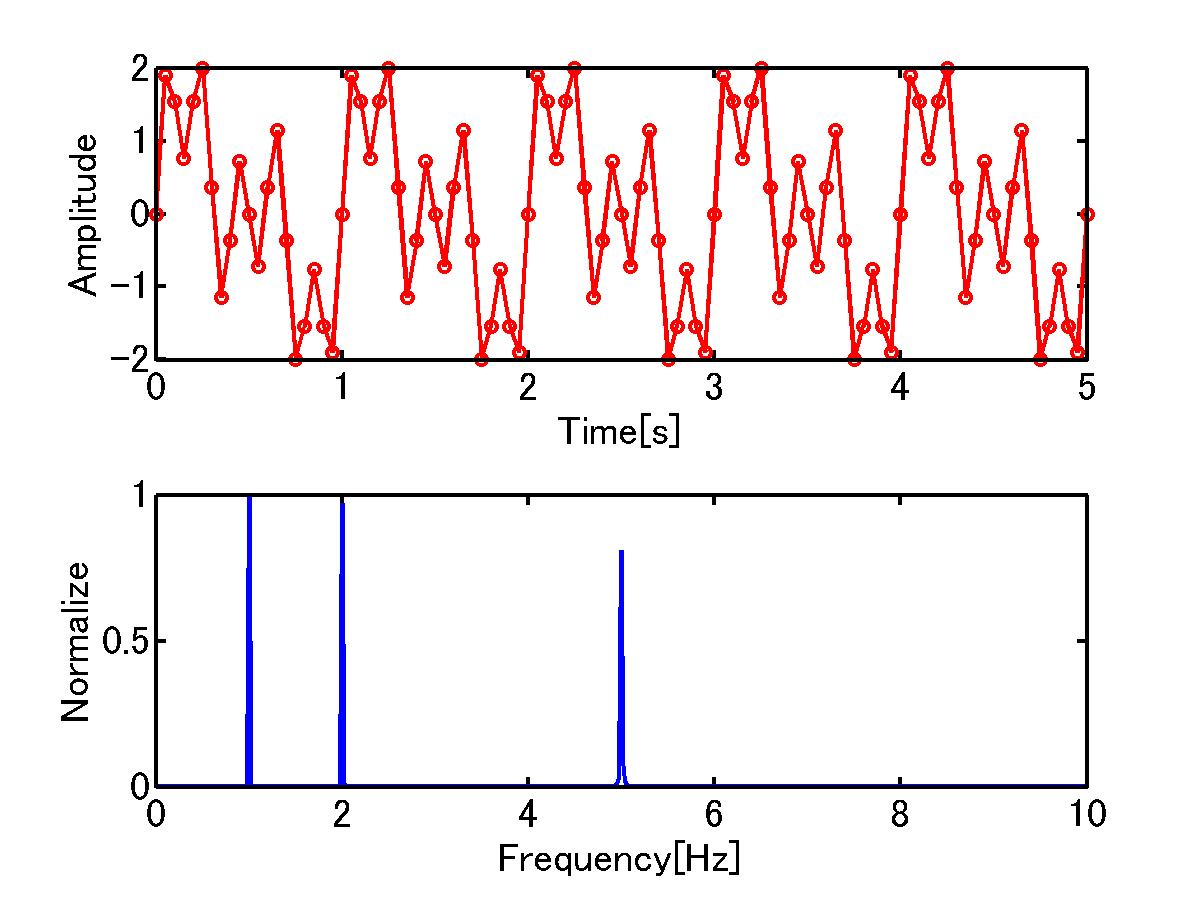
% 1Hz+2Hz+5Hzの正弦波を表示する
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
subplot(2,1,1);
f1=1; %1[Hz]
f2=2; %2[Hz]
f3=5; %5[Hz]
if 1
y1=sin(2*pi*f1*t);
else
y1=zerodata; %0でもうまくいく
end
if 1
y2=sin(2*pi*f2*t);
else
y2=0;
end
if 1
y3=sin(2*pi*f3*t);
else
y3=0;
end
y=y1+y2+y3;
% 1+2+5Hzの正弦波を表示する
plot(t,y,'ro-','linewidth',2);
%stem(t,y,'ro-');
hold on;
axis([0 5 -Inf Inf]);
h=gca;
set(h,'LineWidth',2,...,
'FontSize',15);
xlabel('Time[s]','Fontsize',15);
ylabel('Amplitude','Fontsize',15)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 周波数スペクトルを表示する
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
subplot(2,1,2);
data=[];
%基本周波数の導出 基本周波数=サンプリング周波数/データ数
basicfre = df/retu
%FFTの結果は複素数である。複素数はテキストデータで保存できない
fftdata = fft(y(1:retu))';
%分解して、テキストとして保存する
fftdata_re = real(fftdata);
fftdata_im = imag(fftdata);
%離散周波数を作る
data = [data,[0:retu-1]'*df/retu];
%FFTの実部を格納する
data = [data,fftdata_re];
%FFTの虚部を格納する
data = [data,fftdata_im];
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 周波数スペクトルの絶対値を求める
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%FFTの絶対値を求める
power=abs(fftdata).^2;
maxpower = max(power);
%Normalize(正規化する)
Nmpower = power/maxpower;
%Normalize + [dB/dec]
NmpowerDB = 20*log10(power/maxpower);
%正規化データを格納する
data = [data,Nmpower];
%正規化データ[dB/dec]を格納する
data = [data,NmpowerDB];
plot(data(:,1),data(:,4),'b-','linewidth',2);
axis([0 df/2 0 1]);
h=gca;
set(h,'LineWidth',2,...,
'FontSize',15);
xlabel('Frequency[Hz]','Fontsize',15);
ylabel('Normalize','Fontsize',15);
save fftdata.txt data -ascii
print -djpeg fft_sample.jpg

周波数 FFTの実部 FFTの虚部 FFTの絶対値 FFTの絶対値[dB/dec] 0.0000000e+000 -8.5997875e-013 -0.0000000e+000 2.9701028e-030 -5.9054457e+002 1.9980020e-002 1.0238257e-004 3.2621866e-002 4.2738365e-009 -1.6738364e+002 3.9960040e-002 4.0986708e-004 6.5296747e-002 1.7123646e-008 -1.5532808e+002 5.9940060e-002 9.2346767e-004 9.8078048e-002 3.8634755e-008 -1.4826044e+002 7.9920080e-002 1.6448870e-003 1.3101996e-001 6.8950813e-008 -1.4322921e+002 9.9900100e-002 2.5765350e-003 1.6417786e-001 1.0827599e-007 -1.3930936e+002 1.1988012e-001 3.7215561e-003 1.9760876e-001 1.5687814e-007 -1.3608875e+002 1.3986014e-001 5.0838652e-003 2.3137174e-001 2.1509300e-007 -1.3334747e+002 1.5984016e-001 6.6681924e-003 2.6552845e-001 2.8332961e-007 -1.3095416e+002
データはこのような形で保存しておくとあとで利用しやすい。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
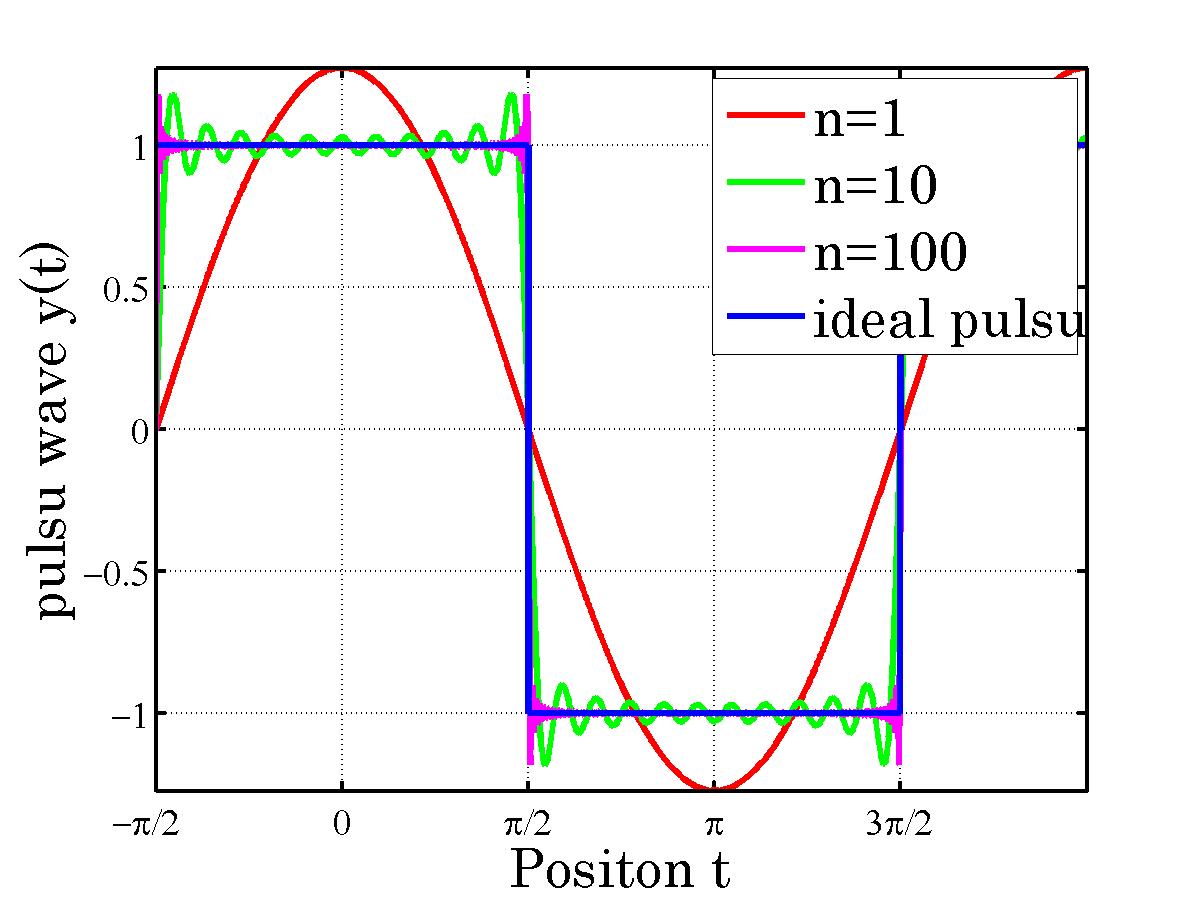
% パルス波形を表示
% programming by embedded samurai
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
echo off
clear all
close all
%サンプリング周期 1[ms]
dx=1e-3;
% xの範囲は -pi/2から0.001単位で2piまで
x=[-pi/2:dx:2*pi];
xx = x/pi;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 注意!
% cos(n*x) n=omega
% n=omega=1,2,..,n である。
% omega = 2*pi*f = 1,2,...,n の意味なので
% 周波数的には、
% f= 1/2pi,2/2pi,3/2pi,...,n
% = 0.1592[Hz],0.3183[Hz],0.4775[Hz],0.6366[Hz],
% = 0.7958[Hz],0.9549[Hz],1.1141[Hz],....,n
%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 1[Hz]を表示
% ここはテスト
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
figure(1);
ty1=sin(2*pi*1*x);
%1[Hz]に近い
ty2=sin(6.2832*x);
plot(xx,ty1,'r-','linewidth',2);
hold on;
plot(xx,ty2,'b--','linewidth',3);
% xラベルとその文字の大きさ、線の太さの設定
str={'-p/2','0','p/2','p','3p/2','2p'}
set(gca,'FontName','symbol','xtick',[-0.5:.5:2],'xticklabel',str)
set(gca,'LineWidth',2,'FontSize',18)
% x-y範囲
axis([-Inf Inf -Inf Inf]);
grid on
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% n=1のとき
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
figure(2);
y1=0;
for m=0:1:0
y=(4/pi)*(1/(2*m+1))*(-1)^m*cos((2*m+1).*x);
y1=y1+y;
end
plot(xx,y1,'r-','linewidth',3);
hold on;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% n=10のとき
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
y2=0;
for m=0:1:10
y=(4/pi)*(1/(2*m+1))*(-1)^m*cos((2*m+1).*x);
y2=y2+y;
end
plot(xx,y2,'g-','linewidth',3);
hold on;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% n=100のとき
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
y3=0;
for m=0:1:100
y=(4/pi)*(1/(2*m+1))*(-1)^m*cos((2*m+1).*x);
y3=y3+y;
end
plot(xx,y3,'m-','linewidth',3);
hold on;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 理想パルス
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
data=[];
for n=x
if (n < pi/2)
y=1;
data=[data,y];
elseif (n >= pi/2) && (n <= 3*pi/2)
y=-1;
data=[data,y];
elseif ( n > 3*pi/2)
y=1;
data=[data,y];
end
end
plot(xx,data,'b-','linewidth',3);
hold on;
% xラベルとその文字の大きさ、線の太さの設定
str={'-p/2','0','p/2','p','3p/2','2p'}
set(gca,'FontName','symbol','xtick',[-0.5:.5:2],'xticklabel',str)
set(gca,'LineWidth',2,'FontSize',18)
% x-y範囲
axis([-Inf Inf -Inf Inf]);
grid on
% xラベル、yラベル
xlabel('Positon t','Fontsize',20,'FontName','Century');
ylabel('pulsu wave y(t)','Fontsize',20,'FontName','Century')
% キャプション
h=legend('n=1',...,
'n=10',...,
'n=100',...,
'ideal pulsu',...,
1);
set(h,'FontSize',20,'FontName','Century');
print -djpeg pulsuwave_t.jpeg
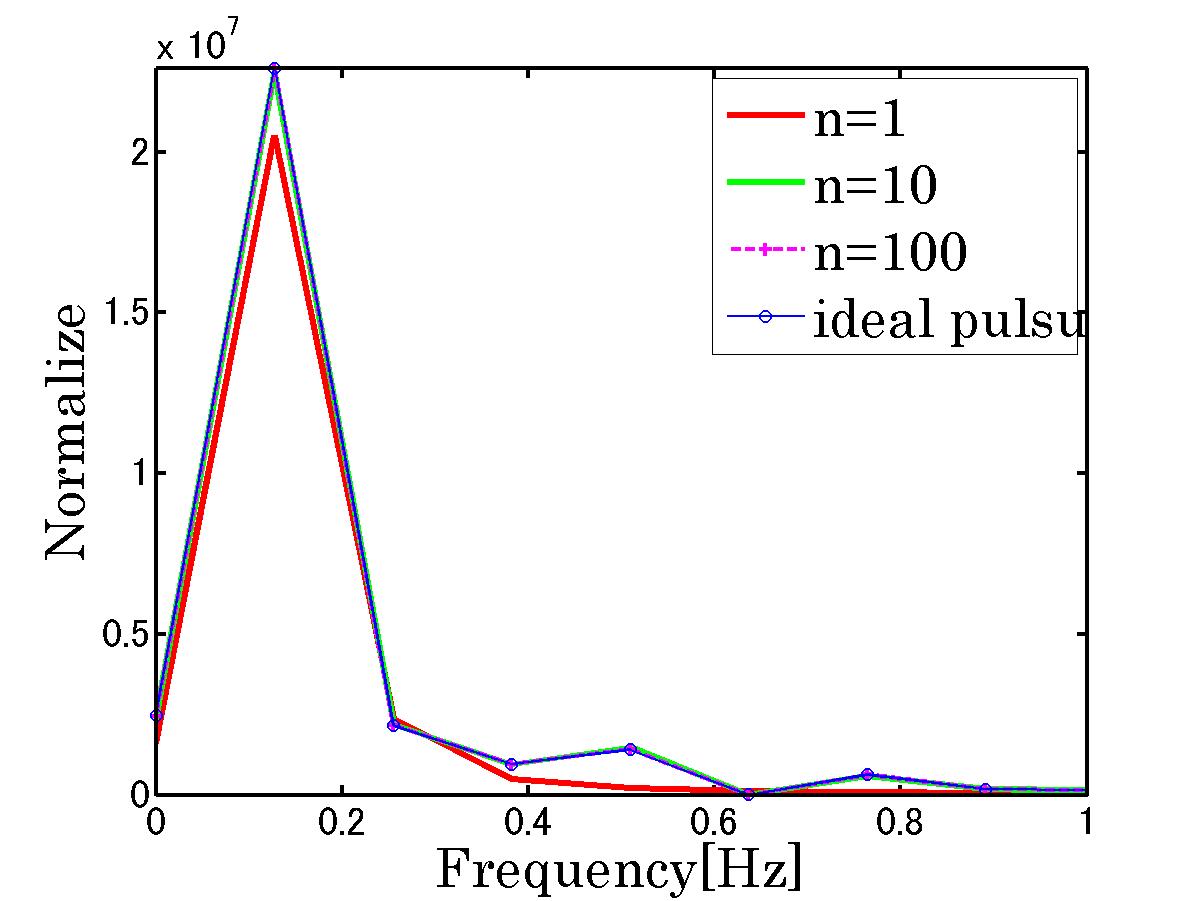
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
figure(3);
%サンプリング周波数 1kHz
df=1/dx
%xの数 7854
[gyo retu]=size(x)
%基本周波数 0.1273[Hz]
bf=df/retu
%FFTの結果は複素数である
fftdata1 = fft(y1)';
fftdata2 = fft(y2)';
fftdata3 = fft(y3)';
fftdata4 = fft(data)';
%FFTの絶対値を求める
power1=abs(fftdata1).^2;
power2=abs(fftdata2).^2;
power3=abs(fftdata3).^2;
power4=abs(fftdata4).^2;
%離散周波数を作る
freq = [0:retu-1]'*bf
plot(freq,power1,'r-','linewidth',3);
hold on
plot(freq,power2,'g-','linewidth',3);
hold on
plot(freq,power3,'m+--','linewidth',2);
hold on
plot(freq,power4,'bo-','linewidth',1);
hold on
axis([0 1 0 Inf]);
set(gca,'LineWidth',2,...,
'FontSize',15);
xlabel('Frequency[Hz]','Fontsize',20,'FontName','Century');
ylabel('Normalize','Fontsize',20,'FontName','Century');
% キャプション
h=legend('n=1',...,
'n=10',...,
'n=100',...,
'ideal pulsu',...,
1);
set(h,'FontSize',20,'FontName','Century');
print -djpeg pulsuwave_f.jpg