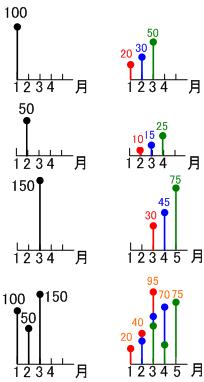
いま、上の図のようにその月に100個仕入れると、
その月は20個来月は30個さ来月は50個
売れる商品があります。
このように商品の売れ行きが分かっている
(つまり未来の状況があらかじめ予測できる)
ならば、
1月に100個
2月に50個
3月に150個
仕入れると、
1月に20個
2月に40個
3月に95個
4月に70個
5月に75個
売れることが予測できます。
グラフをもう一度見てみましょう。
つまり、その月に入荷した個数が、左の割合で出荷していくと考えることができます。
これをプログラムしてみましょう。
まずデータを
1月 2月 3月 4月 5月
x[5]={100, 50, 150, 0, 0 };
としましょう。
つまり、x[2](3月)が現在ならば、x[1](2月)、x[0](1月)は過去を表しています。
それでは、1月,2月,3月,4月,5月の出荷数を計算してみます。
一般式は下記で表されます。
![y[n]= \sum_{k=0}^{N-1} (h[k] x[n-k])](BEF6B9FEA4DFA4CBA4C4A4A4A4C6_eq0001.gif "y[n]= \sum_{k=0}^{N-1} (h[k] x[n-k])")
= ![h[0]x[n-0] + h[1]x[n-1] + h[2]x[n-3] + ... + h[N-1]x[n-(N-1)]](BEF6B9FEA4DFA4CBA4C4A4A4A4C6_eq0002.gif "h[0]x[n-0] + h[1]x[n-1] + h[2]x[n-3] + ... + h[N-1]x[n-(N-1)]")
予測できる係数h[N]が決まれば計算できそうです。
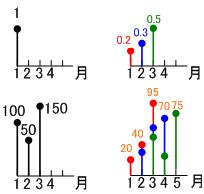
hn[3]={0.2, 0.3, 0.5};
x[5]={100, 50, 150, 0,0 };
ここで
hn[3]=0.2 ... その月の予想
0.3 ... 1か月後の予想~
0.5 ... 2か月後の予想~
です。2か月先まで予想できるわけですね。
一般式はこうなります。
![y[n]= \sum_{k=0}^{2} h[k] x[n-k]](BEF6B9FEA4DFA4CBA4C4A4A4A4C6_eq0003.gif "y[n]= \sum_{k=0}^{2} h[k] x[n-k]")
![= h[0]x[n-0] + h[1]x[n-1] + h[2]x[n-2]](BEF6B9FEA4DFA4CBA4C4A4A4A4C6_eq0004.gif "= h[0]x[n-0] + h[1]x[n-1] + h[2]x[n-2]")
では計算します。
===============================================
■1月の計算です。
y[0] = h[0]*x[0] + h[1]x[-1] + h[2]x[-2];
= 0.2*100 + 0.3*0 + 0.5*0;~
= 20;
1月(現在) x "1月の予想" = "1月の出荷"~
ここでx[-1],x[-2]は,1か月前及び2か月前のデータですが、
データは1月から始まってますのでこれはゼロとみなすことができます。
を表しています。
========================================================
■2月の計算です。
y[n] = h[0]x[n-0] + h[1]x[n-1] + h[2]x[n-2];
y[1] = h[0]*x[1] + h[1]x[0] + h[2]x[-1];
= 0.2*50 + 0.3*100 + 0.5*0;
= 10 + 30
= 40;
2月(現在) x "2月の予想" = "2月の出荷" + 1月(ひとつ前の過去) x "1月からの1か月後の未来予想" = 1月の入荷から予想される"2月の出荷"
を表しています。
=========================================================
■3月の計算です。
y[n] = h[0]x[n-0] + h[1]x[n-1] + h[2]x[n-2];
y[2] = h[0]*x[2] + h[1]x[1] + h[2]x[0];
= 0.2*150 + 0.3*50 + 0.5*100;
= 30 + 15 + 50
= 95;
3月(現在) x "3月の予想" = "3月の出荷" + 2月(1つ前の過去) x "2月からの1カ月後の未来予想" = 2月の入荷から予想される"3月の出荷" + 1月(2つ前の過去) x "1月からの2か月後の未来予想" = 1月の入荷から予想される"3月の出荷"
を表しています。
============================================================
■4月の計算です。
y[n] = h[0]x[n-0] + h[1]x[n-1] + h[2]x[n-2];
y[3] = h[0]*x[3] + h[1]x[2] + h[2]x[1];
= 0.2*0 + 0.3*150 + 0.5*50;
= 0 + 45 + 25
= 70;
4月(現在) x "4月の予想" = "4月の出荷" + 3月(1つ前の過去) x "3月からの1カ月後の未来予想" = 3月の入荷から予想される"4月の出荷" + 2月(2つ前の過去) x "2月からの2カ月後の未来予想" = 2月の入荷から予想される"4月の出荷"
を表しています。
============================================================
■5月の計算です。
y[n] = h[0]x[n-0] + h[1]x[n-1] + h[2]x[n-2];
y[4] = h[0]*x[4] + h[1]x[3] + h[2]x[2];
= 0.2*0 + 0.3*0 + 0.5*150;
= 75;
5月(現在) x "5月の予想" = "5月の出荷" + 4月(1つ前の過去) x "4月からの1カ月後の未来予想" = 4月の入荷から予想される"5月の出荷" + 3月(1つ前の過去) x "3月からの2カ月後の未来予想" = 3月の入荷から予想される"5月の出荷"
を表しています。
================================================================
■6月の計算です。
y[n] = h[0]x[n-0] + h[1]x[n-1] + h[2]x[n-2];
y[5] = h[0]*x[5] + h[1]x[4] + h[2]x[3];
= 0.2*0 + 0.3*0 + 0.5*0;
= 0;
6月(現在) x "6月の予想" = "6月の出荷" + 5月(1つ前の過去) x "5月からの1カ月後の未来予想" = 5月の入荷から予想される"6月の出荷" + 4月(1つ前の過去) x "4月からの2カ月後の未来予想" = 4月の入荷から予想される"6月の出荷"
を表しています。
ここで重要なこと係数の個数分のデータが入力として与えられたとき、出力は正常に出力されると考えられます。
係数の個数分以下のデータが入力として与えられたとき、それは過度状態と等価と考えられます。
例えば、係数3で、データが1つしかない場合、
現在は1つ前の過去からの予測と2つ前の過去からの予測と現在の予測からなりたっているため、
1つ前及び2つ前の予測が定まらないためこの状態を過度状態と呼びます。
この場合は1月の結果 20ヶ及び2月の結果 40ヶはそれが本当かどうか分かりません。
この1月,2月のデータはあてになりません。
つまり、
現在は過去が分からないと不安定になってしまいます。
逆に線形性が成り立てば未来は予測できるのです。
)
また、
結果は、5月まで出力しています。5月,4月のデータがないにもかかわらず...。
これは存在したデータの最後、つまり3月のデータと2ヶ月後の未来予想の結果が
残っているからです。
そのためMatlabのconv関数では係数+2個のデータまで出力してくれます。
しかしながら4月、5月のデータもまたあまりあてにはできないことに注意してください!
1月,2月及び4月,5月はあてにできず、3月のみあてにできそうということが分かります。
この例では、
1月,2月は過度状態としてあてにはできませんが、4月,5月はデータを用意していないため
あてにできていないことが分かります。
つまり、
フィルタの出力は
データが係数個用意されたときの2つ後のデータから有効となり
また
係数と同じ量のデータは常に最新のものに置き換わらないとその後のデータは有効とならない
ということが分かります。
1月 2月 3月 4月 5月
x[5]={100, 50, 150, 0, 0 };
は、
100 0 0 0 0 50 100 0 0 0 150 50 100 0 0 - 150 50 100 0 <--dataを入れ続けないといけない！ - - 150 50 100 <--dataを入れ続けないといけない！
それを加味するとC言語のコードは以下のようになります。
一般にグラフの横軸が正のときで、5月までプロットしてある場合は、
5月まで知っていることになるわけですから5月が現在とすると,
1月は4ヶ月前の過去になるわけです（あたりまえのことですが大事です)
つまり静止したグラフの場合は、最新が右側となります。
オシロスコープなどの動いているグラフの場合これも最新は右側になります。
そして過去は左になります。
つまりオシロの場合は、右から左にデータが流れているといえるのです。
#include <stdio.h>
int main(void){
int k=0;
int count=0;
int currentData;
double x[3]={0,0,0};
double hn[3]={0.2, 0.3, 0.5};
const int hn_length=3;
int yn=0;
count=1;
while(1){
printf("現在のデータを入れてください\n");
scanf("%d",¤tData);
x[0]=(double)currentData;
yn=0;
for(k=0;k<hn_length;k++){
yn = yn+(int)(hn[k]*x[k]);
}
printf("y[%d]=%d\n",count++,yn);
//バッファの更新
for(k=hn_length-1;k>0;k--) x[k] = x[k-1];
}//end of while
return 0;
}
現在のデータを入れてください 100 y[1]=20 現在のデータを入れてください 50 y[2]=40 現在のデータを入れてください 150 y[3]=95 現在のデータを入れてください 0 y[4]=70 現在のデータを入れてください 0 y[5]=75 現在のデータを入れてください 0 y[6]=0 現在のデータを入れてください 0 y[7]=0 現在のデータを入れてください 0 y[8]=0 現在のデータを入れてください
係数が
hn[3]={0.2, 0.3, 0.5};
でデータが
x=[100 50 150 200 30 100 500]
のように入ってきたとき、結果yは、
y=[20 40 95 110 141 129 145]
となります。データを更新した場合には4月、5月のデータもこのように変わっていきます。
これをMatlabでやってみましょう。
Matlabのconvを使う場合、あらかじめデータと係数が分かっていなければならない。
その場合
x=[100 50 150 200 30 100 500] 古いデータ 新しいデータ
となる。
ところがさきほど説明したとおり、結果yは、
(1) 係数個番目以上が真の値 (2) 入力データは常に更新しないと係数個より未来の値は真値にならない。
ためデータを更新しながら係数番目のyの値を取り出す必要がある。
hn=[0.2 0.3 0.5];
[hnm hnn]=size(hn);
buffer=[100 50 150 200 30 100 500];
[M N]=size(buffer);
x=zeros(hnm,hnn);
for i=1:1:N
x(hnn)=buffer(i)
ybuf=conv(hn,x);
y=ybuf(hnn)
for j=1:1:hnn-1
x(j) = x(j+1);
end
end
■結果
>> test_conv x = 0 0 100 y = 20 x = 0 100 50 y = 40 x = 100 50 150 y = 95 x = 50 150 200 y = 110 x = 150 200 30 y = 141 x = 200 30 100 y = 129 x = 30 100 500 y = 145
function y=myconv(hn,x)
[M N]=size(hn);
anum=zeros(M,2);
hn=cat(2,hn,anum)
N=N+2;
y=zeros(M,N);
[MX NX]=size(x);
if(NX < N)
anum=zeros(MX,N-NX);
x=cat(2,x,anum)
end
for n=1:1:N
for k=1:1:N
num=n+1-k;
if(num<1)
y(n)=y(n);
else
y(n)=y(n)+hn(k)*x(num);
end
end
end