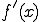 の形で表されているときの積分値を求める
の形で表されているときの積分値を求める
(1)「電気・電子工学のための数値計算法入門」橋本修著 総合電子出版社
(2)「ディジタル信号処理技術」玉井徳みち、長島厚、藤田泰弘、若井修造著 日経BP社
http://szksrv.isc.chubu.ac.jp/java/physics/rlc/rlc0.html
http://www.asahi-net.or.jp/~jk2m-mrt/kiso_RLC.htm
http://ja.wikipedia.org/wiki/%E4%B8%89%E8%A7%92%E9%96%A2%E6%95%B0
特に詳しい(ここを参考にすること)
http://www.cmplx.cse.nagoya-u.ac.jp/~furuhashi/education/CircuitMaker/chap1.pdf
http://www.akita-nct.ac.jp/~yamamoto/lecture/2003/5E/lecture_5E/diff_eq/node2.html
http://chemeng.on.coocan.jp/cemath/cemath08.html
http://homepage3.nifty.com/skomo/f6/hp6_3.htm
http://homepage1.nifty.com/gfk/rungekutta.htm
(a) 微分の説明
微分方程式の解を求める
(b) 微分方程式の解を数値計算で求める
(c) 積分の説明
(d) 関数が微分の形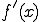 の形で表されているときの積分値を求める
の形で表されているときの積分値を求める
(一般的に数値積分をする意味は、関数自体が変化の式(例えば速度の関数)などで表されているとき
ある時刻から時刻までの距離を求めたいときなどで使用される。
もちろんその変化の式が、手計算によって計算可能ならば積分によって時間と距離の関係を導出し
その時間を入れることで直接距離を導いたほうが早い。
しかし、一般的に時間と距離の関係のような式自体が導出することが不可能な場合が世の中には多く
時間と速度の関係のような変化の式を見つけ出すことの方が容易なのだが、これを手計算で積分すること
は非常に難しいため数値積分が提案された)
微分とは簡単にいうと傾きである
ではそれを説明しましょう。
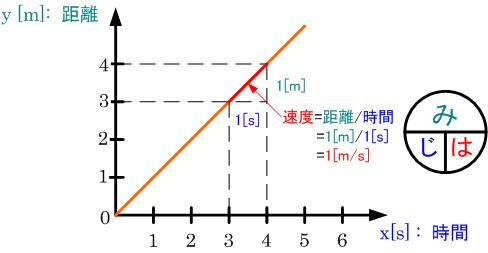
図は横軸に時間を、縦軸に距離をとったグラフです。
時間が1[s]進むごとに1[m]ずつ進んでいることが直感的に分かります。
ではこのグラフから時間が分かると何[m]進むか数式で表してみます。
時間に何かをかけると距離になるといいですよね。
いま分かっているのは時間[s]と距離[m]だけです。
時間を距離に変換するには [m/s] * [s] = [m] ...(1)
つまり距離を時間で割ったものを何かにするとよいわけです。
この[m/s]の正しい関係が分かればよいわけですね。
いま、時間が2[s]進むと距離は2[m]進みますので、
距離を時間で割った傾き
2[m]/2[s] = 1[m/s] ...(2)
1[m/s]というものを時間にかけてやると距離が出ます。
小学生で習う問題です。
この距離[m]を時間[s]で割った傾きを速度[m/s]と言います。
いまこの問題では、傾きはどの区間でもとめても同じ1[m/s]となります。
この傾きがどの区間でも一定となるものを''線形''であるといいます。
速度が分かれば、
距離をy 時間をx 速度をa
とすると
y=ax
という式でこの3つの関係を表すことができる。いまa=1だから
y=x
となる。
ある入力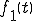 を入力したときの出力を
を入力したときの出力を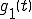 とする。
とする。
別の入力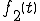 を入力したときの出力を
を入力したときの出力を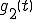 とする。
とする。
2つの信号が同時に加えられた場合の出力は、それぞれの出力を単純に加算したものとなる場合 このシステムは''線形''であるという。
数式で表すと、
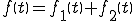
なる入力が加えられるとき
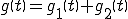
が成り立つ性質を線形性という。
上記のグラフでは、
x' =1[s]のときy' =1[m] x''=3[s]のときy''=3[m]
なので、
x = x' + x'' = 4
のとき
y = y' + y'' = 4
となる。
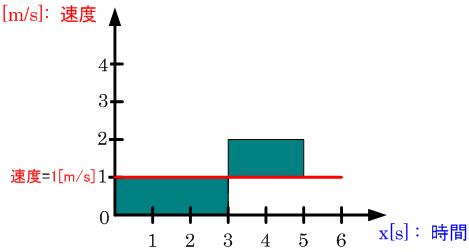
一旦、速度が分かってしまえば、速度に時間をかければ距離になります。
それは、縦軸に速度、横軸に時間をとったときの面積の値と考えることができます。
たとえば、
0[s]から3[s]の間に進んだ距離は、
(1[m/s] x 3[s]) - (1[m/s] x 0[s]) = 3[m]
となり、
3[s]から5[s]の間に進んだ距離は、
(1[m/s] x 5[s]) - (1[m/s] x 3[s]) = 2[m]
となる。
では、速度に線形性、つまり速度が変化する場合はどうなるか?
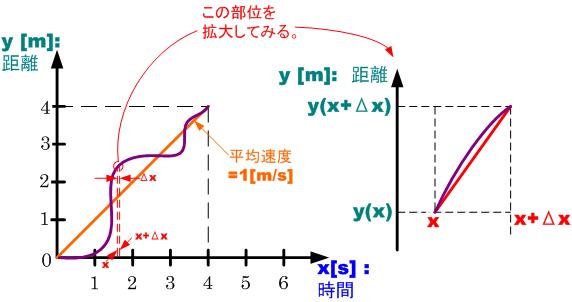
図は4秒間で4[m]に到達しているので、速度は1[m/s]と表してよいだろうか?
最初の0から1秒間の間などはまったくといいほど進んでいない(速度0.000?[m/s])。
1秒から2秒の間ではいっきに2[m]くらい進んでいる(速度2.???[m/s])。
つまり時間において刻々と速度が変化している。
このようなモデルの速度はどのように表したらよいのだろうか?
もともと、距離は速度に時間をかけてやればでてくる。
しかしいま速度は変化しているので、ある時刻における速度に時間をかけてやることで
ある時間における距離が分かる状態になっている。
つまりある時刻における速度を求めることができればよい。
いま時刻![x[s] x[s]](C8F9CAAC40A4BDA4CE3140C8F9CAACA4C8A4CFA4CAA4CBA4AB_eq0008.gif) における距離
における距離![y(x)[m] y(x)[m]](C8F9CAAC40A4BDA4CE3140C8F9CAACA4C8A4CFA4CAA4CBA4AB_eq0009.gif) に注目する。
に注目する。
そこから微小に離れた位置を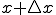 とすると、
とすると、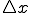 が0に非常に近いほど小さいのなら、
が0に非常に近いほど小さいのなら、
紫の曲線は、赤の直線に近似できるはずである(つまり関数は1次関数となる)。
つまり可能な限り短い時間間隔を取れば、正確な速度に近づく
ここで時間は、
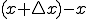
距離は、
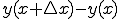
となるので、
速度は、
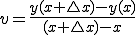
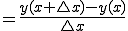
となります。この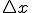 を限りなくゼロにすることで正確な速度に近づくので、
を限りなくゼロにすることで正確な速度に近づくので、
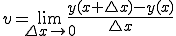
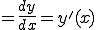
と表す。この操作を微分と呼びます。
つまり微分とはある注目する区間における傾きを表していると考えることができます。
そしてその注目する区間は非常に小さいので1点における傾きを表していると考えられ
それはつまりその点での接線の傾きを表していると考えることができるわけです。
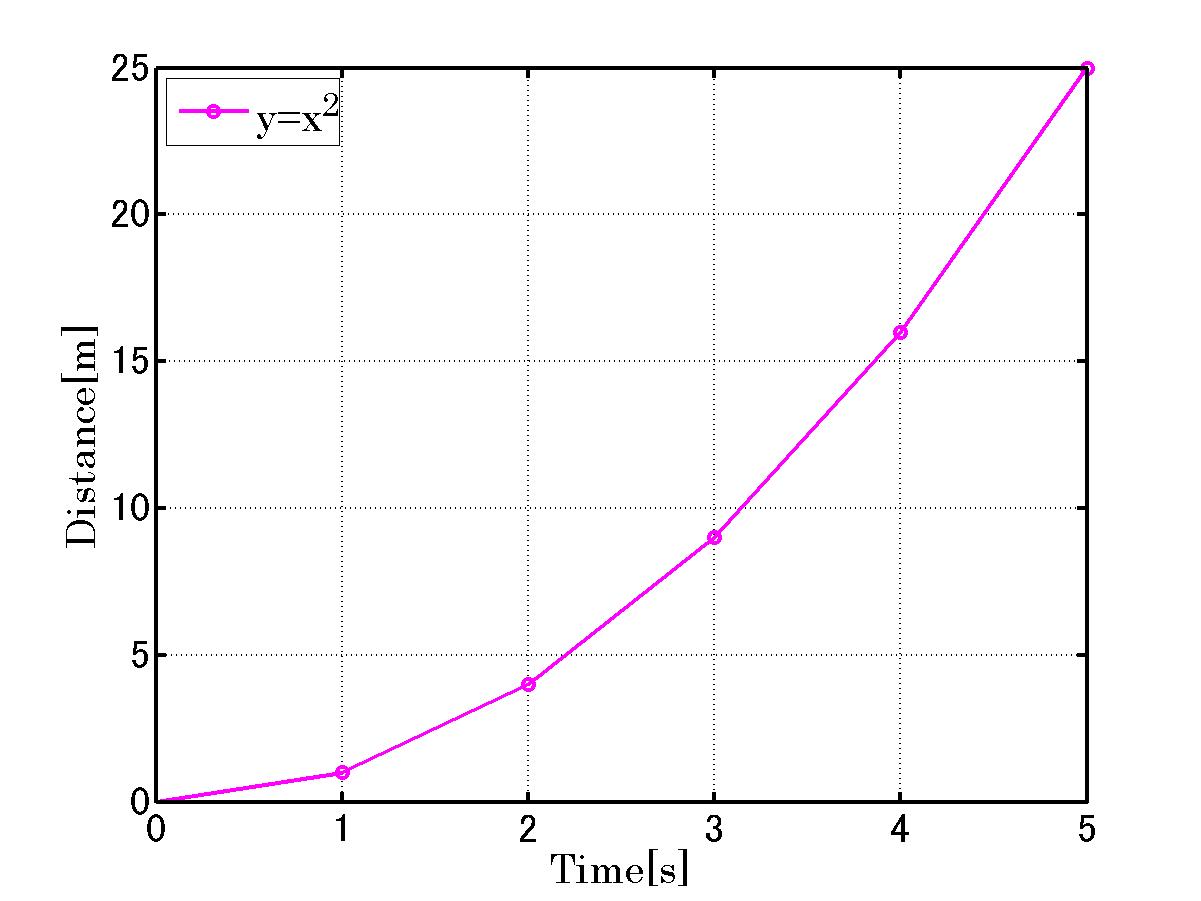
図のような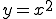 を微分してみましょう。
を微分してみましょう。
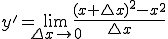
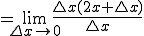
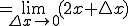
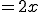
となります。
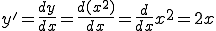
となります。