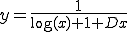 �̌`�ŕ\����Ă���Ƃ��̐ϕ��l�����߂�
�̌`�ŕ\����Ă���Ƃ��̐ϕ��l�����߂�
(1)�u�d�C�E�d�q�H�w�̂��߂̐��l�v�Z�@����v���{�C���@�����d�q�o�Ŏ�
(2)�u�f�B�W�^���M�������Z�p�v�ʈ䓿�݂��A�������A���c�O�A���C���� ���oBP��
(3)�u�悭�킩��L���v�f�@�v���X�h���� Ohmsha
http://szksrv.isc.chubu.ac.jp/java/physics/rlc/rlc0.html
http://www.asahi-net.or.jp/~jk2m-mrt/kiso_RLC.htm
http://ja.wikipedia.org/wiki/%E4%B8%89%E8%A7%92%E9%96%A2%E6%95%B0
http://www.cmplx.cse.nagoya-u.ac.jp/~furuhashi/education/CircuitMaker/chap1.pdf
http://www.akita-nct.ac.jp/~yamamoto/lecture/2003/5E/lecture_5E/diff_eq/node2.html
http://chemeng.on.coocan.jp/cemath/cemath08.html
http://homepage3.nifty.com/skomo/f6/hp6_3.htm
http://homepage1.nifty.com/gfk/rungekutta.htm
(a) �����̐���
�����������̉������߂�
(b) �����������̉��𐔒l�v�Z�ŋ��߂�
(c) �ϕ��̐���
(d) ���������̌`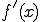 �̌`�ŕ\����Ă���Ƃ��̐ϕ��l�����߂�
�̌`�ŕ\����Ă���Ƃ��̐ϕ��l�����߂�
(��ʓI�ɐ��l�ϕ�������Ӗ��́A�����̂��ω��̎�(�Ⴆ�Α��x�̊�)�Ȃǂŕ\����Ă���Ƃ�
���鎞�����玞���܂ł̋��������߂����Ƃ��ȂǂŎg�p�����B
������̕ω��̎����A��v�Z�ɂ���Čv�Z�\�Ȃ�ΐϕ��ɂ���Ď��ԂƋ����̊W�o��
���̎��Ԃ����邱�ƂŒ��ڋ��������ق��������B
�������A��ʓI�Ɏ��ԂƋ����̊W�̂悤�Ȏ����̂����o���邱�Ƃ��s�\�ȏꍇ�����̒��ɂ͑���
���ԂƑ��x�̊W�̂悤�ȕω��̎��������o�����Ƃ̕����e�ՂȂ̂����A�������v�Z�Őϕ����邱��
�͔��ɓ�����ߐ��l�ϕ�����Ă��ꂽ)
���̐Ď��������́A���̂悤�ɂ��ĉ������Ƃ��o����B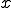 �@���P���I��0 �łȂ��Ƃ��A��������ό`���āA
�@���P���I��0 �łȂ��Ƃ��A��������ό`���āA
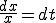
���ӂ�ϕ�����A
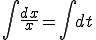
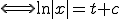
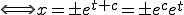
������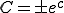 �Ƃ���A
�Ƃ���A
���̕������̉��� 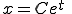 �i
�i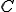 ��0���܂ޔC�ӂ̎����j�ƂȂ�B
��0���܂ޔC�ӂ̎����j�ƂȂ�B
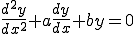
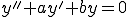
���̔���@�Q�̈ꎟ�Ɨ��ȉ�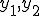 �������Ĉ�ʉ��͂����̈ꎟ�����ƂȂ�B
�������Ĉ�ʉ��͂����̈ꎟ�����ƂȂ�B
(��{���@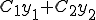 )
)
���ꎟ�Ɨ����̔���
�����L�X�A��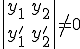
������
| �P�[�X | ��{�� | ��ʉ� |
�@�قȂ�2���� 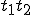 |
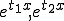 |
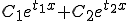 |
�A�d�� 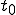 |
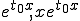 |
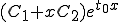 |
�B2���� 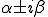 (a,b����) (a,b����) |
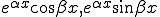 |
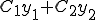 |
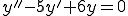
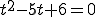
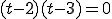
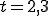
Ans.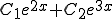
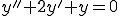
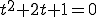
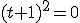
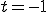
Ans.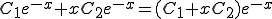
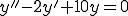
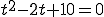
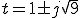
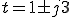
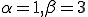
Ans.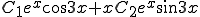
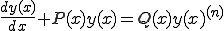 (3-1)
(3-1)
�̂悤�Ȍ`�̔������������x���k�[�C�̔����������ƌĂԁB
������
n=0 �̂Ƃ��͐��`����������
n=1�ȏ�̂Ƃ��͕ϐ����U�`
�ł���B
�Ⴆ�A
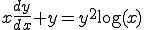
�́A
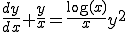
�ƂȂ�̂�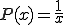
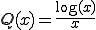
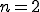
�ƂȂ�B
���āA����
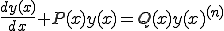 (3-1)
(3-1)
�ƕ\����Ă���Ƃ��́A
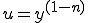 (3-2)�Ƃ�����
(3-2)�Ƃ�����
x��u�̔����������ɂ���������
(3-2)����������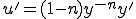
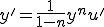 (3-3)
(3-3)
(3-3)��(3-1)�ɑ�������
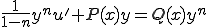
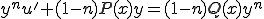
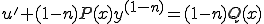
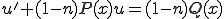 (3-4)
(3-4)
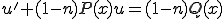 (3-4)
(3-4)
���̂悤�Ƀx���k�[�C�̔�����������(3-4)���̂悤�ɕϐ��ϊ������B
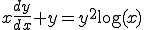
�́A
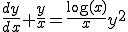
�ƂȂ�̂�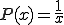
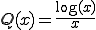
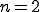
�ƂȂ�B�ϐ��ϊ������
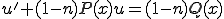 (3-4)
(3-4)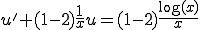
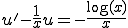 (3-5)
(3-5)
(3-5)����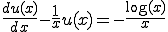 (A-1)
(A-1)
�Ɠ����Ȃ̂ŁA
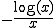 ��0�̂Ƃ��̉����܂��l����(�ߓx��)
��0�̂Ƃ��̉����܂��l����(�ߓx��)
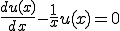 �Ƃ��̉�
�Ƃ��̉�
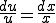
���ӂ�ϕ�����A
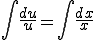
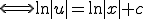
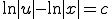
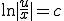
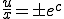
������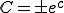 �Ƃ���A
�Ƃ���A
���̕������̉��� 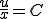
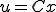 (A-2)
(A-2)
(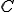 ��0���܂ޔC�ӂ̎����j�ƂȂ�B
��0���܂ޔC�ӂ̎����j�ƂȂ�B
(A-2)�̐ϕ��萔C��x�̊��Ƃ����
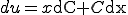 (A-3)
(A-3)
(A-3)��(A-1)�ɑ������
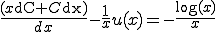 (A-4)
(A-4)
(A-2)��(A-4)�ɑ������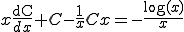
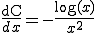
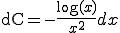
���ӂ�ϕ�����A
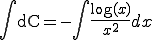
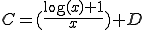 (
(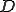 ��0���܂ޔC�ӂ̎���(�ϕ��ϐ�)) (A-5)
��0���܂ޔC�ӂ̎���(�ϕ��ϐ�)) (A-5)
(A-2)��(A-5)���������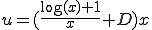
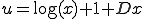 (A-6)
(A-6)
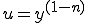 (3-2)�Ƃ�����
(3-2)�Ƃ�����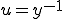 �Ȃ̂�
�Ȃ̂�