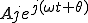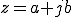 (aとbは実数)
(aとbは実数)
シミュレーティングで学ぶアナログ&ディジタルフィルタ入門 小野浩司著
複素数 z
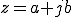 (aとbは実数)
(aとbは実数)
共役複素数 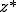
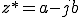
複素数の極座標形式は以下となる。
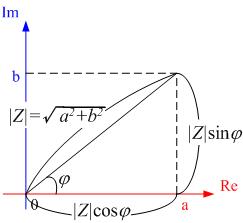
複素数の絶対値|z|は、
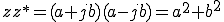
より
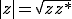
また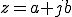
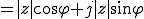
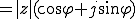
また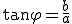
なので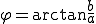
となる。
この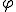 は、複素平面上で偏角と呼ばれる。
は、複素平面上で偏角と呼ばれる。
注意!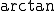 が返す値は、
が返す値は、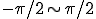 だが、
だが、
複素数では、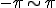
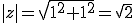
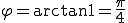
ゆえに
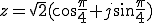
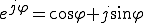 (eは自然対数の底)
(eは自然対数の底)
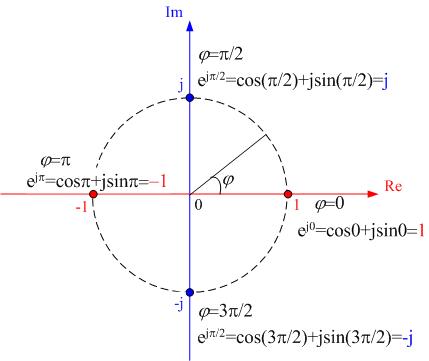
■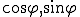 のもとめかた
のもとめかた
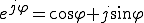 (1)
(1)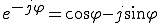 (2)
(2)
(1) + (2)
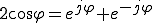
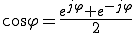
(1) - (2)
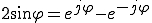
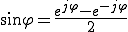
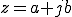
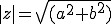
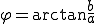
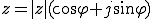 (1)
(1)
(1)は、
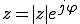 (2)
(2)
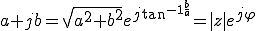
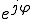 の絶対値
の絶対値
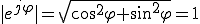
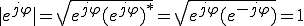
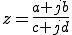 をオイラーの公式を用いて表す。
をオイラーの公式を用いて表す。
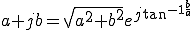
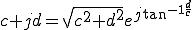
なので
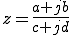
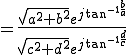
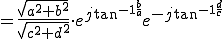

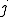 を掛ける操作は
を掛ける操作は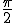 回転させる操作と同じ
回転させる操作と同じ
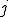 を掛ける操作は
を掛ける操作は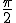 回転させる操作と同じ
回転させる操作と同じ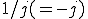 を掛ける操作は
を掛ける操作は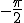 回転させる操作と同じ
回転させる操作と同じ
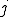 と
と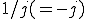 を極形式で表現する
を極形式で表現する
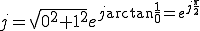
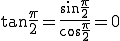
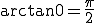
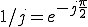
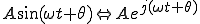
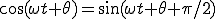
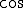 は、
は、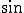 よりも
よりも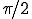 位相が進んでいる(左にずれている)。
位相が進んでいる(左にずれている)。
(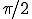 回転しているのと同じ);なので、
回転しているのと同じ);なので、
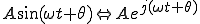
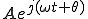 に位相進み分、つまりjをかけてやればいい。
に位相進み分、つまりjをかけてやればいい。