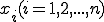 としたとき、
としたとき、平均(算術平均)
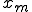 は、個々の測定値の総和を求め、
は、個々の測定値の総和を求め、それを総数で割ればでる。
つまり、
参考文献 「電気電子工学のための数値計算法入門」橋本修先生
同一量のn回の測定値を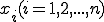 としたとき、
としたとき、
平均(算術平均)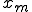 は、個々の測定値の総和を求め、
は、個々の測定値の総和を求め、
それを総数で割ればでる。
つまり、
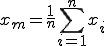
集団xの平均値を表す時は、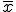 と表す。
と表す。
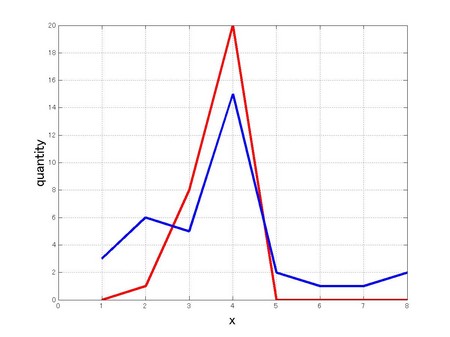
今図のように平均値が4だがデータの分布の度合いが違う赤と青の集団があるとする。図を見ると、互いに同じ平均値を持っているが、分布状態がまるで違うことがわかる。そこで、
平均値とは別に集団の分布のバラツキを表すものがあればそれもまた集団の構造を表す指標となる
赤で示す図では、5,6,7,8のデータはどれも0だが青線ではデータが少しずつ存在している。
そこで、個々のデータと平均値との差をとれば、なんとなくバラツキぐあいを数式で表現できそうである。
この各測定値から平均値を引いたものを偏差と呼ぶ。
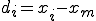
この偏差を全てのxについて計算し、その総和を取ればバラツキの尺度が得られそうな気がするが、実際にやってみると偏差のプラス値とマイナス値が打ち消しあって、その総和は常にゼロになってしまう。
このことこそが平均値の性質であり、平均値とは偏差の総和がゼロになることであるのだ。
そこで、
バラツキの尺度を求めるために、偏差の符号を消す->2乗する
その2乗した偏差をデータの総数で割ればバラツキが求められる。
そのバラツキの尺度を分散と呼び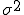 で表される。
で表される。
(母集団の分散ということで母分散ともいう)
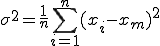
母分散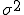 が母集団のバラツキを表す尺度であるからその平方根
が母集団のバラツキを表す尺度であるからその平方根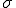 もまた母集団のバラツキの尺度を表すはずである。
もまた母集団のバラツキの尺度を表すはずである。
この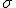 を標準偏差(母標準偏差)と呼ぶ。
を標準偏差(母標準偏差)と呼ぶ。
幾何学的に2乗する事は面積を表し、その平方根は線分を意味してる。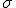 はその計算式において、平均変化率と解釈でき、これは微分係数としての意味を持っている。
はその計算式において、平均変化率と解釈でき、これは微分係数としての意味を持っている。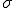 は、平均変化率が変化する点(変曲点)から分布の中心(平均値)までの距離を表している。
は、平均変化率が変化する点(変曲点)から分布の中心(平均値)までの距離を表している。
このことにより、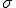 の大きさによって分布の形状が分かる.
の大きさによって分布の形状が分かる.
1つのものを繰り返し測定した場合、その測定値の分布は平たい分布(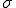 が大きい)より尖った分布(
が大きい)より尖った分布(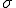 が小さい)の方が精度が良いと言える。
が小さい)の方が精度が良いと言える。
幾つものデータを寄せ集めた場合に、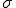 が大きいと裾広がりな多様な分布であり、
が大きいと裾広がりな多様な分布であり、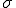 が小さいと平均値に集中している分布と言える。
が小さいと平均値に集中している分布と言える。
同じ条件で測定を繰り返すと、偶然誤差のために測定値は確率分布を取るが測定回数が多くなると、正規分布(ガウス分布)に近づいていく。
測定値が正規分布を取るとき、測定値がxとx+dxの間になる確率をp(x)dxとするとき、
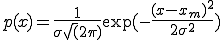
を確率誤差関数という。先ほども書いたが、標準偏差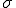 は、平均値を中心とするp(x)の広がりを示し、測定値のばらつきの度合いを表している。また、p(x)は、x=平均値のときに最大値
は、平均値を中心とするp(x)の広がりを示し、測定値のばらつきの度合いを表している。また、p(x)は、x=平均値のときに最大値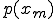 となる。つまり、平均値が測定の最確値である。またp(x)の式は正規化されており、
となる。つまり、平均値が測定の最確値である。またp(x)の式は正規化されており、
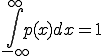
である。この数式の意味は測定値の存在確率が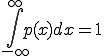 から
から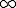 までみたとき必ず存在することを意味している。
までみたとき必ず存在することを意味している。
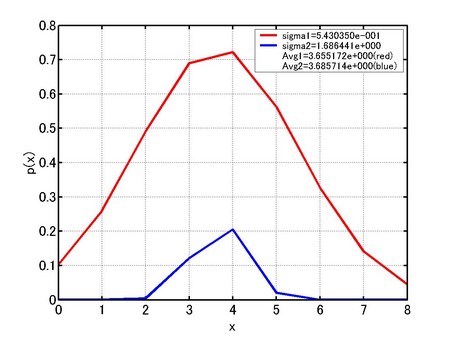
この確率誤差関数のグラフの見方をおさらいしよう。
例えば、測定値4というデータが全測定値の中にどのくらいの割合で存在するかを見るとすると、赤のグラフでは約70%の確率で4が存在することが分かるのである。逆に測定値8などは5%の確率で存在するだろうということが分かる。
つまり、この確率誤差関数とは各々の測定値の存在確率を示している。
以下に確認用Matlabスクリプトを示す。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 平均、分散、標準偏差
% written by embedded.samurai
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
echo off
clear all
close all
%平均が4になるようなデータを作る
x1=[ 3 4 4 4 2 4 4 4 3 3 4 4 4 4 4 3 4 3 4 4 4 4 4 3 3 4 4 4 3];
x2=[ 1 2 8 4 4 2 4 5 4 4 3 2 4 4 3 4 4 2 3 3 4 3 4 4 4 1 4 1 4 6 8 2 2 7 5 ];
%rowには行、columnには列の個数が入る。
[row1 column1]=size(x1);
[row2 column2]=size(x2);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Step1. 平均値からのばらつきをグラフ化する。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
for count=1:1:column1
x1_data(count)=0;
end
for count=1:1:column1
x1_data(x1(count)) = x1_data(x1(count))+1;
end
for count2=1:1:column2
x2_data(count2)=0;
end
for count2=1:1:column2
x2_data(x2(count2)) = x2_data(x2(count2))+1;
end
figure(1)
max1= max(x1)
max2= max(x2)
i1 = [0:1:max1];
i2 = [0:1:max2];
plot(x1_data,'r-','linewidth',3);
hold on
plot(x2_data,'b-','linewidth',3);
grid on
xlabel('x','Fontsize',18)
ylabel('quantity','Fontsize',18)
axis([0 8 0 20]);
print -djpeg distribute.jpeg
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Step2. 確率誤差関数を求める。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%値の合計を作る
%for count=1:1:column
% sum=sum+x1(count);
%end
sum1 = sum(x1);
sum2 = sum(x2);
%平均値(算術平均)を求める
avg1 = sum1/column1
avg2 = sum2/column2
%個々の値の偏差を求める
di1 = x1 - avg1
di2 = x2 - avg2
%バラツキの尺度を求めたい
%test=0;
%for i=1:1:column
% test = test + di(i);
%end
%test
%偏差のプラス値とマイナス値が打ち消しあって、その総和は常にゼロになる。
%平均値とは偏差の総和がゼロになることである。
%バラツキの尺度を求めるために、偏差の符号を消す->2乗する
%その2乗した偏差をデータの総数で割ればバラツキが求められる。
%そのバラツキの尺度を分散と呼び\sigma^2で表される。
%(母集団の分散ということで母分散ともいう)
%分散を求める
%sigma2=0;
%for count=1:1:column
% sigma2 = sigma2 + di(count)^2;
%end
sigma2_1 = sum(di1.^2);
sigma2_2 = sum(di2.^2);
sigma2_1 = sigma2_1/column1
sigma2_2 = sigma2_2/column2
%母分散\sigma^2が母集団のバラツキを表す尺度であるから
%その平方根\sigmaもまた母集団のバラツキの尺度を表す。
%この\sigmaを標準偏差(母標準偏差)と呼ぶ。
%標準偏差を求める
sigma_1 = sqrt(sigma2_1)
sigma_2 = sqrt(sigma2_2)
%幾何学的に2乗する事は面積を表し、その平方根は線分を意味してる。
%\sigmaはその計算式において、平均変化率と解釈でき、
%これは微分係数としての意味を持っている。
%\sigmaは、平均変化率が変化する点(変曲点)から分布の中心(平均値)
%までの距離を表している。
%このことにより、\sigmaの大きさによって分布の形状が分かる.
%1つのものを繰り返し測定した場合、
%その測定値の分布は平たい分布(\sigmaが大きい)
%より尖った分布(\sigmaが小さい)の方が精度が良いと言える。
%幾つものデータを寄せ集めた場合に、
%\sigmaが大きいと裾広がりな多様な分布であり、
%\sigmaが小さいと平均値に集中している分布と言える。
%確率誤差関数を求める
max1= max(x1)
max2= max(x2)
i1 = [0:1:max1];
i2 = [0:1:max2];
p1 = 1/(sigma_1*sqrt(2*pi))*exp(-((i2-avg1).^2 / 2*sigma2_1));
hold on;
p2 = 1/(sigma_2*sqrt(2*pi))*exp(-((i2-avg2).^2 / 2*sigma2_2));
figure(2)
plot(i2,p1,'r-','linewidth',3);
hold on
plot(i2,p2,'b-','linewidth',3);
grid on
xlabel('x','Fontsize',18)
ylabel('p(x)','Fontsize',18)
cavg1 = sprintf('Avg1=%d(red)',avg1);
csigma1 = sprintf('sigma1=%d',sigma_1);
cavg2 = sprintf('Avg2=%d(blue)',avg2);
csigma2 = sprintf('sigma2=%d',sigma_2);
h=legend(csigma1,...,
csigma2,...,
cavg1,...,
cavg2,...,
1);
set(h,'FontSize',13)
h=gca
set(h,'LineWidth',2,...,
'FontSize',18)
print -djpeg dispersion.jpeg