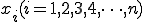 での関数値
での関数値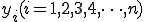 が与えられたとき、
が与えられたとき、これら全ての点
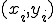 を通る曲線の方程式を求め
を通る曲線の方程式を求めその方程式から任意のxに対する関数値を近似する方法を補間という。
n個の異なる点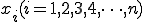 での関数値
での関数値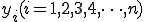 が与えられたとき、
が与えられたとき、
これら全ての点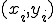 を通る曲線の方程式を求め
を通る曲線の方程式を求め
その方程式から任意のxに対する関数値を近似する方法を補間という。
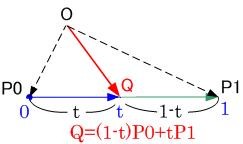
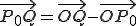
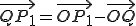
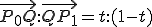
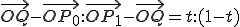
簡単化のため視点Oを省略する。
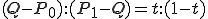
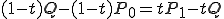
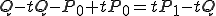
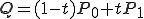
線形補間とは、tを0から1までに動かしたときのQの値を求めることで、
P0からP1までの間の点を補ってやることである。
○プログラム例
Point linerInterpolation(double t)
{
point.x=(int)(x0*(1.0-t) + x1*t);
point.y=(int)(y0*(1.0-t) + y1*t);
return point;
}
関数形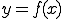 が分からないが、
が分からないが、
独立変数xの離散値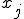 と
と
従属変数yの離散値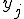 から、
から、
関数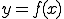 の概形を決定する方法として、
の概形を決定する方法として、
ニュートンの補間法がある。
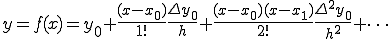
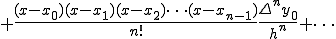
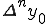 は、n階の前進差分を示す。
は、n階の前進差分を示す。
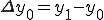
ゆえに、
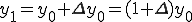
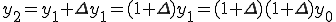
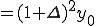
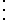
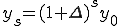 (式1-2)
(式1-2)
ここで二項定理
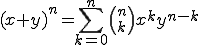
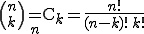
一般の二項定理
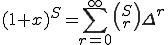
を使うと、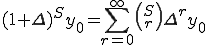
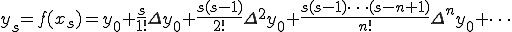 (式1-3)
(式1-3)
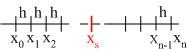
ここで、ある任意の点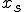 と、
と、
点 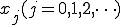
の関係は、図を見ると明らかなように、
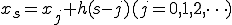
(例
例えば s=4のときの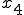 が分かっているとき、
が分かっているとき、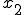 は?
は?
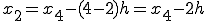
となる。)
この関係は、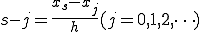
となり、
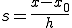
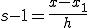
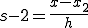
このs,s-1,s-2を式(1-3)に代入すると、ニュートンの補間式を得る。
/*************************************************************/
/* Newton の補間公式 */
/* written by embedded.samurai */
/*************************************************************/
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
double i[]={ -1.122182,
0.841471,
0.539353,
0.0,
0.779067,
2.524414,
3.366545};
double dif[6][7];
int main(void)
{
int n=0;
int m=0;
double e=0.;
double s=0.;
double g2=0.,g4=0.,g6=0.;
FILE *fout;
//file open
fout = fopen("output.txt","w");
// 0 initial
memset(dif,0,sizeof(dif));
//1階差分
for(n=0;n<6;n++){
dif[0][n] = i[n+1]-i[n];
}
//2階差分
for(n=0;n<5;n++){
dif[1][n] = dif[0][n+1] - dif[0][n];
}
//3階差分
for(n=0;n<4;n++){
dif[2][n] = dif[1][n+1] - dif[1][n];
}
//4階差分
for(n=0;n<3;n++){
dif[3][n] = dif[2][n+1] - dif[2][n];
}
//5階差分
for(n=0;n<2;n++){
dif[4][n] = dif[3][n+1] - dif[3][n];
}
//6階差分
for(n=0;n<1;n++){
dif[5][n] = dif[4][n+1] - dif[4][n];
}
e=-1.5;
//出力
printf("y=E[V] x=I(mA) dy d^2y d^3y d^4y d^5y d^6y\n");
for(n=0;n<7;n++){
printf("%+3.1f\t%+7.5f ",e,i[n]);
for(m=0;m<6;m++){
printf("%+7.5f ",dif[m][n]);
}
printf("\n");
e=e+0.5;
}
//ニュートンの前進差分補間公式
for(e=-1.5;e<1.6;e=e+0.1){
s=2.0*e + 3.0; //(x-(-1.5))/0.5 s=(x-x_0)/h
//2階差分
g2 = i[0] + s*dif[0][0] + s*(s-1)*dif[1][0]/2.;
//4階差分
g4 = i[0] + s*dif[0][0] + s*(s-1)*dif[1][0]/2. + s*(s-1)*(s-2)*dif[2][0]/6. + s*(s-1)*(s-2)*(s-3)*dif[3][0]/24.;
//6階差分
g6 = i[0] + s*dif[0][0] + s*(s-1)*dif[1][0]/2. + s*(s-1)*(s-2)*dif[2][0]/6. + s*(s-1)*(s-2)*(s-3)*dif[3][0]/24.
+ s*(s-1)*(s-2)*(s-3)*(s-4)*dif[4][0]/120. + s*(s-1)*(s-2)*(s-3)*(s-4)*(s-5)*dif[5][0]/720. ;
fprintf(fout,"%e %e %e %e\n",e,g2,g4,g6);
}
fclose(fout);
return 0;
}
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% newton interpolation's graph
% written by embedded.samurai
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
echo on
close all
clear all
figure(1)
load('output.txt');
xdata=[-1.5 -1.0 -0.5 0.0 0.5 1.0 1.5];
xdata=xdata';
ydata=[-1.122182 0.841471 0.539353 0.0000 0.779067 2.524414 3.366545];
ydata=ydata';
data=cat(2,xdata,ydata);
plot(data(:,1),data(:,2),'ro','linewidth',2)
%semilogx(output(:,1),output(:,2),'ro-','linewidth',2)
hold on
plot(output(:,1),output(:,2),'b-','linewidth',2)
hold on
plot(output(:,1),output(:,3),'g-','linewidth',2)
hold on
plot(output(:,1),output(:,4),'m-','linewidth',2)
grid on
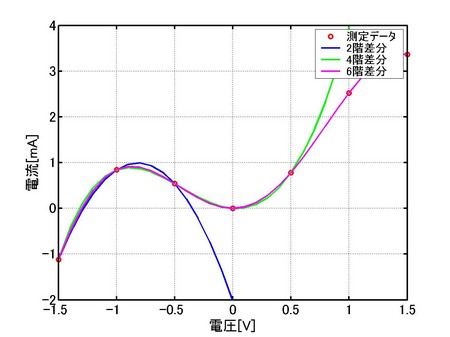
xlabel('電圧[V]','Fontsize',18)
ylabel('電流[mA]','Fontsize',18)
h=legend('測定データ',...,
'2階差分',...,
'4階差分',...,
'6階差分',...,
1);
set(h,'FontSize',15)
h=gca
set(h,'LineWidth',2,...,
'FontSize',18)
%axis([-Inf Inf -Inf Inf]);
axis([ -1.5 1.5 -2 4 ]);
print -djpeg newton_graph.jpeg