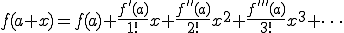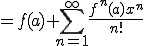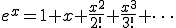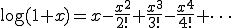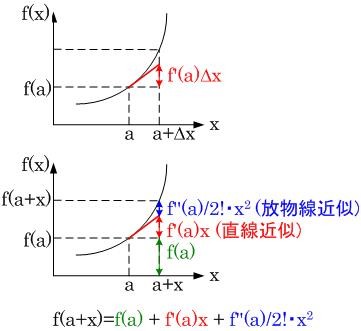

今、x=aのときの関数値f(a)が求められるとするとき、
変数がaからわずかに違う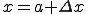 になったときの
になったときの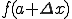 は?
は?
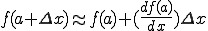
( f(a)が分かっているときf(a)と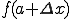 を結ぶ直線をaにおける曲線の接線と等しいとみなす。)
を結ぶ直線をaにおける曲線の接線と等しいとみなす。)
1辺10cmの立方体が熱されて1辺が1mm伸びたときその体積は?
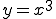
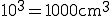
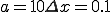
○近似式で解く
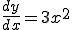
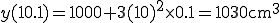
○正確な値は
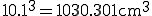
○誤差率は
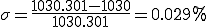
ある曲線は、近似を1次(直線),2次(曲線),3次...というように
無限個の近似曲線の集合によって、もとの曲線に近づけることができる。
これをテーラー展開という。