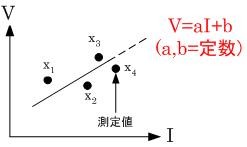

図のようにV(電圧)とI(電流)の複数のデータから一定の関係を見つける問題を考える。
いいかえると次式の最確値a,bを決定する問題となる。
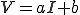 (a,b=定数)
(a,b=定数)
このような問題の解法として最小2乗法がある。
まず1組の測定値が確実に得られるためにはどのようにするかを考えてみよう。
n回の測定値を
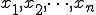 とし、その最確値を
とし、その最確値を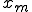 とすると、
とすると、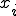 の測定値をうる確率
の測定値をうる確率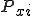
は、確率誤差関数に比例するから、
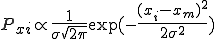
よって、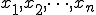 なる測定値が得られる確率は、
なる測定値が得られる確率は、
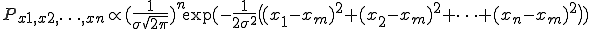 (1-1)
(1-1)
一方、上の一組の測定値が現実に得られることは、得られる確率(1-1)式
において、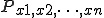 が最大になっているはずである。
が最大になっているはずである。
そのためには分子が最小になればいいから、
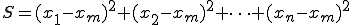
=最小 (1-2)
が成り立てばいい。
ここで例えば平均値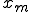 を確実に得たいと考えた場合は、
を確実に得たいと考えた場合は、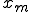 の偏微分を取ればいい。
の偏微分を取ればいい。
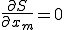 (1-3)
(1-3)
(1-3)式を計算すれば、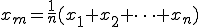 (1-4)
(1-4)
これは、測定値を全部足してそれを総数で割った平均と同じになる。
次に実際にaとbの最確値を求めていこう。
測定量xとyとの間に、簡単のために次の関係があるとし、
xとyの測定値からaとbの最確値を決定する。
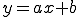 (2-1)
(2-1)
(2-1)式の直線を決めるためにn組の測定値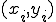 が得られたとき、
が得られたとき、
平均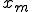 から偏差を求めるように、
から偏差を求めるように、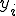 からの偏差を考えると
からの偏差を考えると
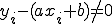 (2-2)
(2-2)
となり、その確率誤差関数P(x)を求めると,
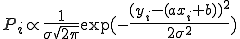 (2-3)
(2-3)
のようになる。
ここから同じようにSが最小になるようにa,bを求めれば最確値a,bが決定する。
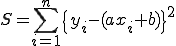 (2-4)
(2-4)
a,bを最小化する条件は、
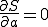 及び
及び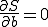 であり、
であり、
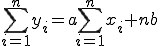 ①
①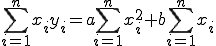 ② (2-5)
② (2-5)
(メモ ①x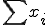 - ②xnでaを計算。)
- ②xnでaを計算。)
そして上式を解いて、a,bは次のように決定される。
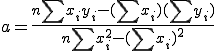
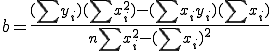
aが決定していればbは、①式より
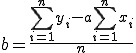
とした方が簡単である。
(2-6)式
また標準偏差は、
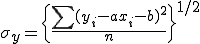 (2-7)
(2-7)
となる。
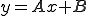 (A,Bは定数)においてxとyを測定して表1.を得たときのAとBの最確値を求める。
(A,Bは定数)においてxとyを測定して表1.を得たときのAとBの最確値を求める。
| *x | 1 | 2 | 3 | 4 |
| *y | 4.5 | 5.7 | 7.3 | 8.5 |
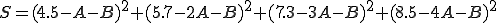
SをA,Bで編微分して0とおくと、次のようになる。
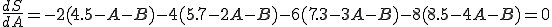
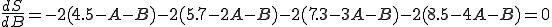
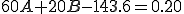
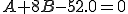
このようにして得られた両式からA=1.36,B=3.10となる。
! least squares method
PROGRAM leastSquaresMethod
implicit none
integer::open_status ! determination open flag
integer:: i,n
real*8::x(100),y(100),sumx,sumy,sumxx,sumxy,a,b
integer::buf
write(*,*) "calculate using least squares method"
!input file
open(9,file='input.txt',iostat=open_status)
if(open_status>0) stop "Input error"
!input data
write(*,*) "input data from input.txt"
n=4
read(9,*) (x(i),y(i),i=1,n)
close(9)
!!!!!!!!!!!!!!!!!!!!!!!!!!
! least squaares method
!!!!!!!!!!!!!!!!!!!!!!!!!
sumx=0
sumy=0
sumxx=0
sumxy=0
do i=1,n
sumx = sumx + x(i)
sumy = sumy + y(i)
sumxx = sumxx + x(i)**2
sumxy = sumxy + x(i)*y(i)
end do
a=(n*sumxy-sumx*sumy) / (n*sumxx-sumx**2)
b=(sumy-a*sumx)/n
write(*,777) 'a=',a,'b=',b
777 format(' ',2(a5,f8.3))
close(9)
stop
end PROGRAM leastSquaresMethod
./test calculate using least squares method input data from input.txt a= 1.360 b= 3.100