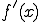 の形で表されているときの積分値を求める
の形で表されているときの積分値を求める
(1)「電気・電子工学のための数値計算法入門」橋本修著 総合電子出版社
(2)「ディジタル信号処理技術」玉井徳みち、長島厚、藤田泰弘、若井修造著 日経BP社
(3)「よくわかる有限要素法」福森栄次著 Ohmsha
http://szksrv.isc.chubu.ac.jp/java/physics/rlc/rlc0.html
http://www.asahi-net.or.jp/~jk2m-mrt/kiso_RLC.htm
http://ja.wikipedia.org/wiki/%E4%B8%89%E8%A7%92%E9%96%A2%E6%95%B0
http://www.cmplx.cse.nagoya-u.ac.jp/~furuhashi/education/CircuitMaker/chap1.pdf
http://www.akita-nct.ac.jp/~yamamoto/lecture/2003/5E/lecture_5E/diff_eq/node2.html
http://chemeng.on.coocan.jp/cemath/cemath08.html
http://homepage3.nifty.com/skomo/f6/hp6_3.htm
http://homepage1.nifty.com/gfk/rungekutta.htm
(a) 微分の説明
微分方程式の解を求める
(b) 微分方程式の解を数値計算で求める
(c) 積分の説明
(d) 関数が微分の形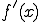 の形で表されているときの積分値を求める
の形で表されているときの積分値を求める
(一般的に数値積分をする意味は、関数自体が変化の式(例えば速度の関数)などで表されているとき
ある時刻から時刻までの距離を求めたいときなどで使用される。
もちろんその変化の式が、手計算によって計算可能ならば積分によって時間と距離の関係を導出し
その時間を入れることで直接距離を導いたほうが早い。
しかし、一般的に時間と距離の関係のような式自体が導出することが不可能な場合が世の中には多く
時間と速度の関係のような変化の式を見つけ出すことの方が容易なのだが、これを手計算で積分すること
は非常に難しいため数値積分が提案された)
積分とは、変化(傾き)の式が分かっている場合に、その各々の点での変化の式と位置
をかけて各々の位置での量を求め、それの総和をとることである区間からある区間までの
量を求める操作である。
図のように時間が分かると距離が分かる場合、積分は必要ありません。
しかしこのうねうねした式が求められない場合の方が世の中には多いのです。
そのときに変化の式が分かっていると(この場合は速度です)
積分を使ってある時間区間の距離が求められるのです。
つまり、この場合は、時間が分かると距離が分かる上記の式が求められない場合、
時間が分かると速度が分かる式を求め、
各々の時間での速度と各々の時間をかけた、各々の時間での各々の距離を
求める時間間隔分足し合わせるのです。
するとある時間間隔での距離が求められるというわけです。
積分の方はひとことで表した意味が把握しにくいのですが、
どう考えたら良いかを次から説明していきます。
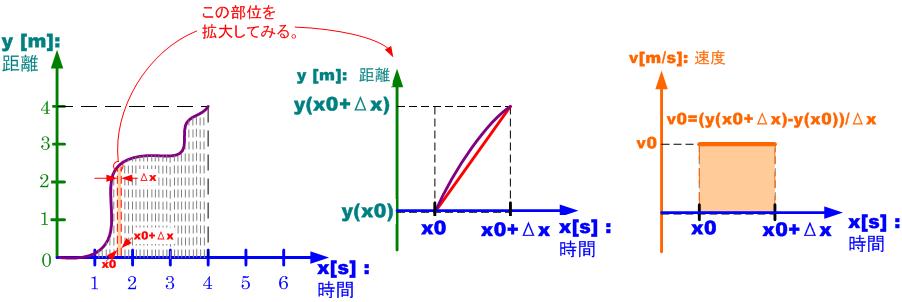
微分とはなにかでは図の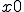 の領域での微分について説明した。
の領域での微分について説明した。
x0での時間での微分においてx0での速度が分かれば、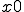 から
から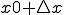 の間の時間
の間の時間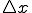 での距離は
での距離は
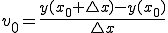
から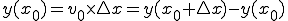
これを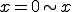 まで足し合わせると
まで足し合わせると![x=0[s] x=0[s]](C0D1CAAC40A4BDA4CE3140C0D1CAACA4C8A4CFA4CAA4CBA4AB_eq0009.gif) から
から![x=x[s] x=x[s]](C0D1CAAC40A4BDA4CE3140C0D1CAACA4C8A4CFA4CAA4CBA4AB_eq0010.gif) 経過したときの距離を出すことができます。
経過したときの距離を出すことができます。
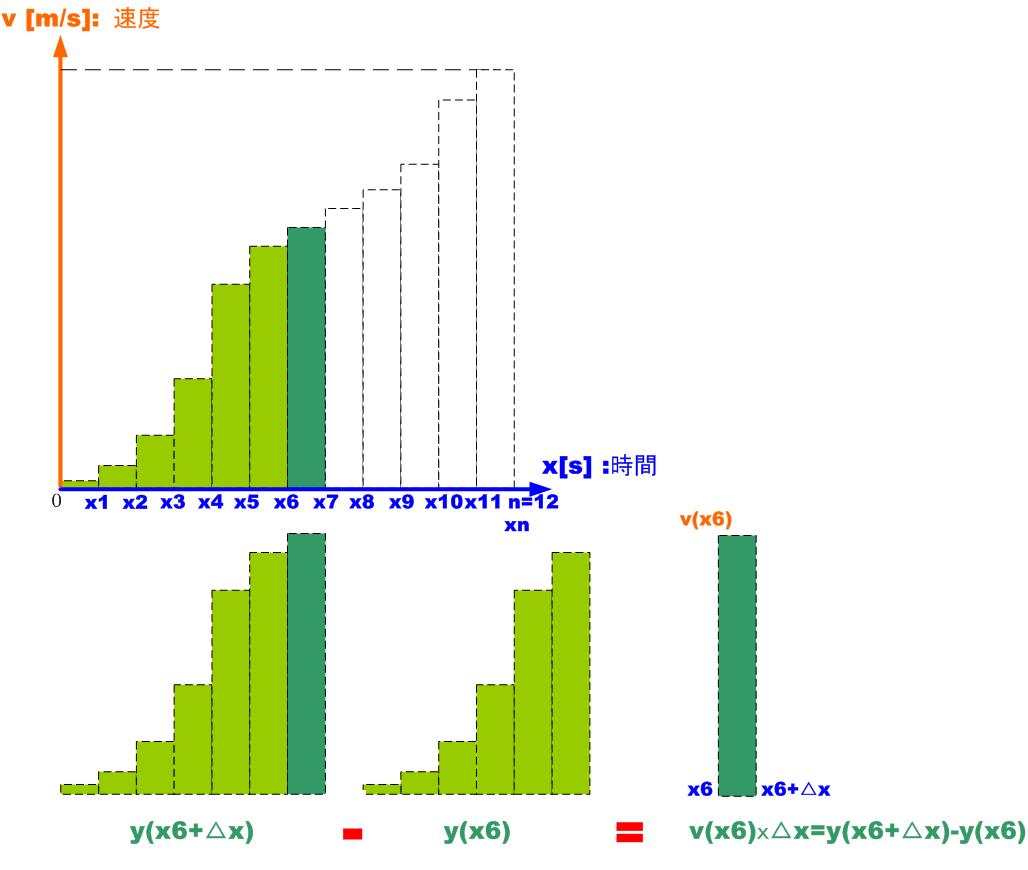
図で少し考えてみましょう。例えば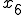 における速度は、
における速度は、
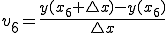
なので、距離は、
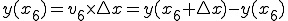
縦軸を各点における速度、横軸を時間とすれば短冊一個が各々の速度と時間をかけた距離となります。
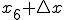 における距離
における距離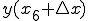 というのは縦軸を速度にしたときは、
というのは縦軸を速度にしたときは、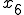 までの各々の点から導いた速度と
までの各々の点から導いた速度と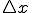 をかけたものをすべて足したものに等しい。
をかけたものをすべて足したものに等しい。
そして
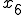 における距離
における距離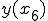 というのは縦軸を速度にしたときは、
というのは縦軸を速度にしたときは、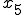 までの各々の点から導いた速度と
までの各々の点から導いた速度と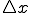 をかけたものをすべて足したものに等しい。
をかけたものをすべて足したものに等しい。
これを引いたものが、
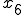 時間での速度
時間での速度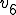 と、距離
と、距離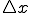 の積と等しい。
の積と等しい。
これは、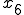 から
から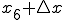 までに動いた距離となります。
までに動いた距離となります。
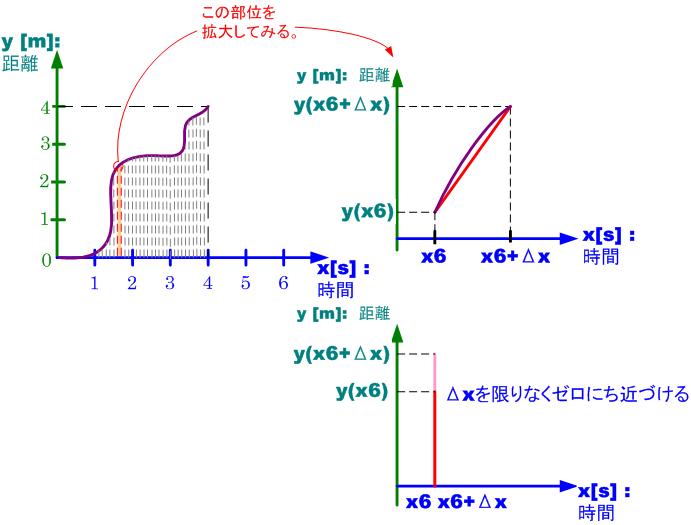
縦軸を距離にしてみれば、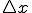 は限りなくゼロに近いので
は限りなくゼロに近いので
単純に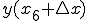 から
から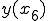 を引いたときが、
を引いたときが、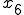 から
から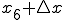 までに動いた距離となることが理解できます。
までに動いた距離となることが理解できます。

さて、先ほどの図に戻ります。
今、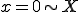 を、N個の区間に分けるとする。
を、N個の区間に分けるとする。
(いまXはN=12の地点のグラフの端とし定数とする。Nもまた定数である。)
すると
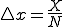 (
(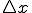 は定数である)
は定数である)
となる。
するとある時刻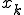 は、(
は、(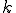 は、
は、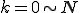 のk番目を示す整数とする)
のk番目を示す整数とする)
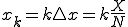
となり、k番目の速度を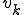 とすると
とすると
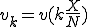 となるので
となるので
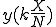 から
から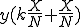 までの距離は、
までの距離は、
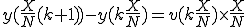
時間が0からxまでに進んだ距離は、各々の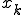 時間における
時間における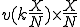
を、0からNまで足せばいいわけだから、
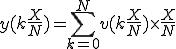
ここで、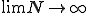 とすると
とすると は限りなく0に近くなるので
は限りなく0に近くなるので
より正確な距離を求めることができます。
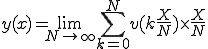 (1-1)
(1-1)
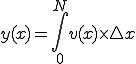 (1-2)
(1-2)
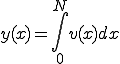 (1-3)
(1-3)
となり、
xまでの距離は、0からNまでのxの各点における速度と微小区間dxをかけて0からNまで足し合わせる。
そのときdxは限りなくゼロに近いですよ
ということを(1-3)は表しています。この表現方法を積分といいます。
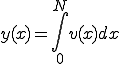 (1-3)
(1-3)
これを計算するわけですが、ここでもう一度グラフを見てみます。

いま、0からXまでの積分を求めるとすると、
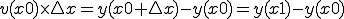
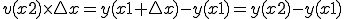
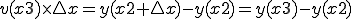
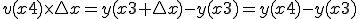
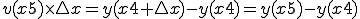
:
: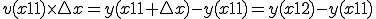
ゆえに
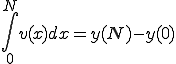 (1-4)
(1-4)
に等しくなります。
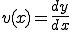
ですので、y(x)の関数の微分を表しています。
ですから、傾きで表された積分は、元の距離の関数を求めて引き算をすればいいということになります。
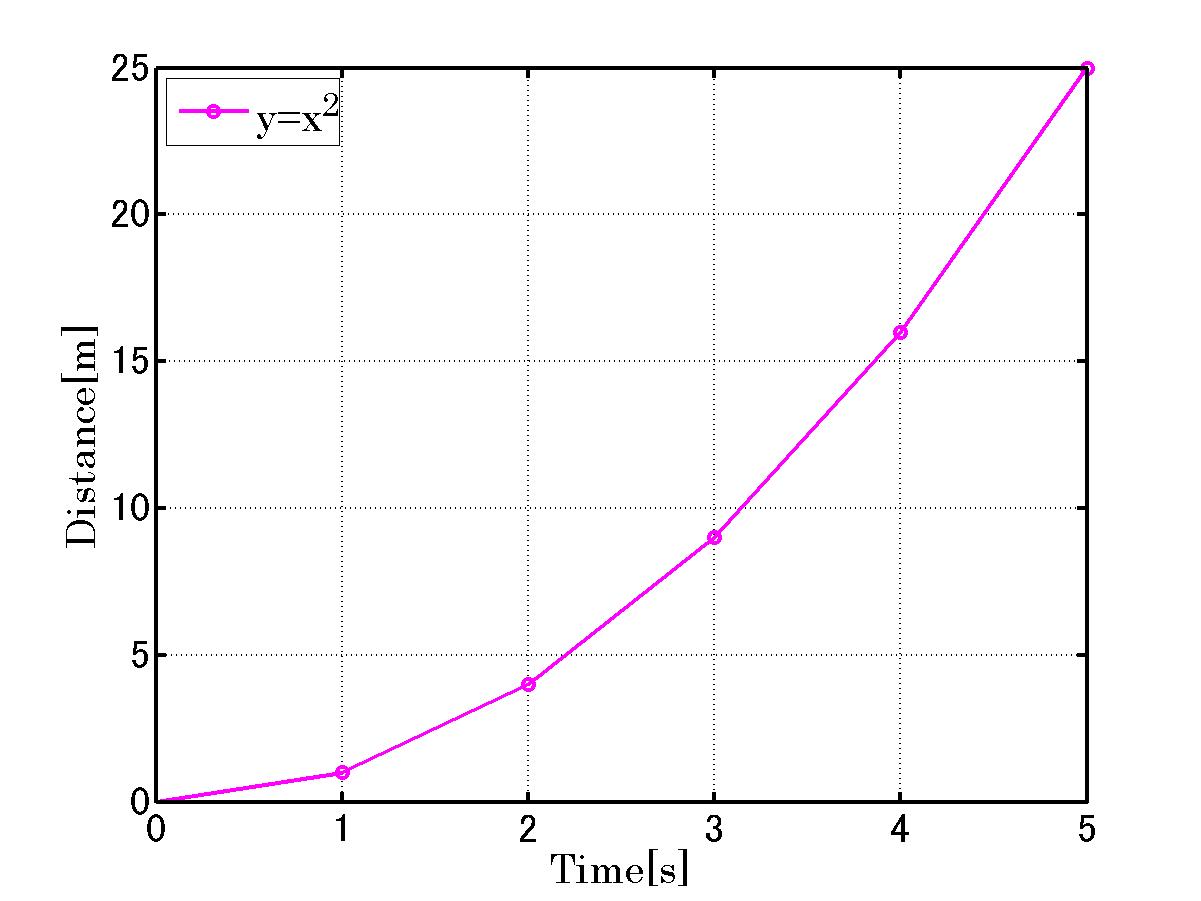
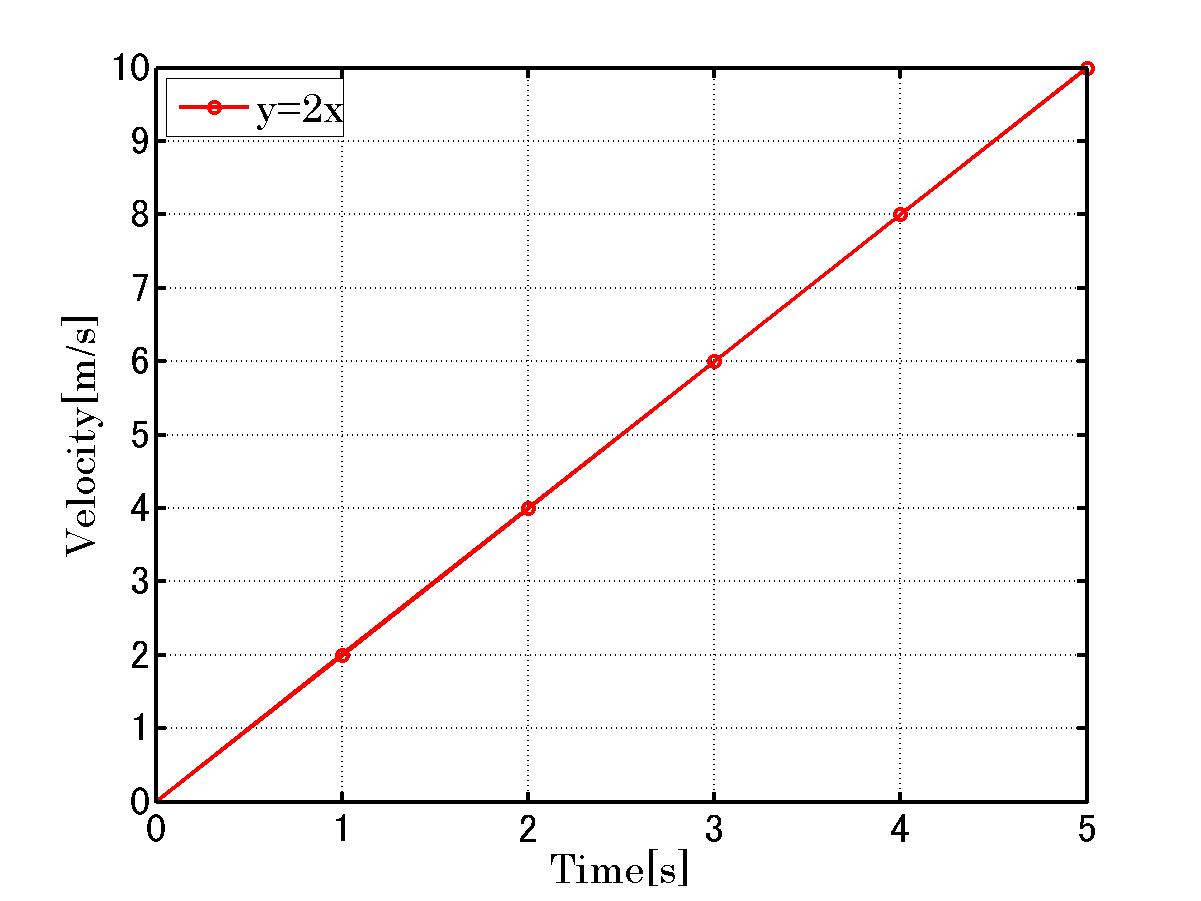
いまxを時間としてyを距離とします。
いま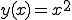 で時間と距離の関係が表されている式があります。
で時間と距離の関係が表されている式があります。
これを微分すると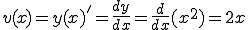
です。これは速度になるわけですね。
さて、いまxを0秒から出発して5秒までに進んだ距離を求めましょう。![y(5) = 5^2 = 25[m] y(5) = 5^2 = 25[m]](C0D1CAAC40A4BDA4CE3140C0D1CAACA4C8A4CFA4CAA4CBA4AB_eq0063.gif)
ですね。
積分で求めると、速度は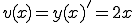 なので
なので
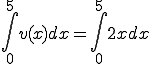
![\int_0^{5} (x^2)' dx = [ x^2 ]^5_0 = 25-0 = 25 \int_0^{5} (x^2)' dx = [ x^2 ]^5_0 = 25-0 = 25](C0D1CAAC40A4BDA4CE3140C0D1CAACA4C8A4CFA4CAA4CBA4AB_eq0066.gif)
計算の仕方としては、微分で表された元の式(原関数といいます)を導いて、
積分の上限から下限を引くといった処理になります。
では右のグラフから各々の速度 x 時間の総和が25になっているか確認してみます。
三角形の面積を求めれば良いから
(底辺 x 高さ / 2) = 5 x 10 /2 = 25
となり両者は等しくなりました。
ここで大事なのは、
時間と速度という関係においての総和が、時間と距離の関係においては単なる引き算になる
ということです。
ですから、積分式が出てきたときには変化の総和に着目していることに注意する必要があります。
足し合わせるつまり面積を求めるのは変化率の関数の方なのです(グラフの右のほうです)。