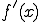 の形で表されているときの積分値を求める
の形で表されているときの積分値を求める
(1)「電気・電子工学のための数値計算法入門」橋本修著 総合電子出版社
(2)「ディジタル信号処理技術」玉井徳みち、長島厚、藤田泰弘、若井修造著 日経BP社
(3)「よくわかる有限要素法」福森栄次著 Ohmsha
http://szksrv.isc.chubu.ac.jp/java/physics/rlc/rlc0.html
http://www.asahi-net.or.jp/~jk2m-mrt/kiso_RLC.htm
http://ja.wikipedia.org/wiki/%E4%B8%89%E8%A7%92%E9%96%A2%E6%95%B0
http://www.cmplx.cse.nagoya-u.ac.jp/~furuhashi/education/CircuitMaker/chap1.pdf
http://www.akita-nct.ac.jp/~yamamoto/lecture/2003/5E/lecture_5E/diff_eq/node2.html
http://chemeng.on.coocan.jp/cemath/cemath08.html
http://homepage3.nifty.com/skomo/f6/hp6_3.htm
http://homepage1.nifty.com/gfk/rungekutta.htm
(a) 微分の説明
微分方程式の解を求める
(b) 微分方程式の解を数値計算で求める
(c) 積分の説明
(d) 関数が微分の形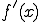 の形で表されているときの積分値を求める
の形で表されているときの積分値を求める
(一般的に数値積分をする意味は、関数自体が変化の式(例えば速度の関数)などで表されているとき
ある時刻から時刻までの距離を求めたいときなどで使用される。
もちろんその変化の式が、手計算によって計算可能ならば積分によって時間と距離の関係を導出し
その時間を入れることで直接距離を導いたほうが早い。
しかし、一般的に時間と距離の関係のような式自体が導出することが不可能な場合が世の中には多く
時間と速度の関係のような変化の式を見つけ出すことの方が容易なのだが、これを手計算で積分すること
は非常に難しいため数値積分が提案された)
ここでは積分を台形法とシンプソン法を用いてプログラムで計算してみます。
台形法は、1つの区間だけを考えます。
シンプソン法は、2つの区間を考えます。
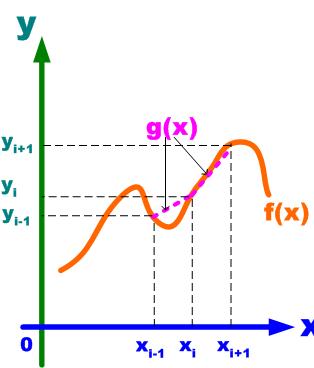
区間[a,b]で連続な関数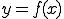 を等間隔にn分割して、その分割点を
を等間隔にn分割して、その分割点を
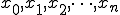 (1-1)
(1-1)
としたとき、その関数曲線上の点
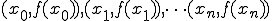 (1-2)
(1-2)
を通る曲線の方程式を近似式で表したもの
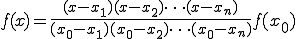
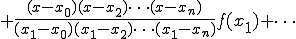
 (1-3)
(1-3)
となります。
ここで、2点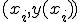 ,
,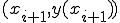
を通る直線を考える。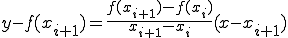
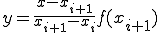
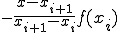
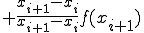
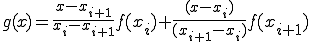 (1-4)
(1-4)
この直線に対して積分すると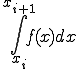
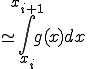
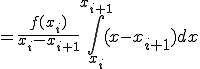
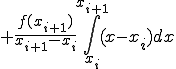
![= \frac{f(x_i)}{x_i - x_{i+1}}\Big[ \frac{1}{2} x^2 - x_{i+1}x \Big]_{x_i}^{x_{i+1}} = \frac{f(x_i)}{x_i - x_{i+1}}\Big[ \frac{1}{2} x^2 - x_{i+1}x \Big]_{x_i}^{x_{i+1}}](BFF4C3CDB7D7BBBB40BFF4C3CDC0D1CAAC40A4BDA4CE3240A5B7A5F3A5D7A5BDA5F3CBA1_eq0019.gif)
![+ \frac{f(x_{i+1})}{x_{i+1} - x_{i}}\Big[ \frac{1}{2} x^2 - x_{i}x \Big]_{x_i}^{x_{i+1}} + \frac{f(x_{i+1})}{x_{i+1} - x_{i}}\Big[ \frac{1}{2} x^2 - x_{i}x \Big]_{x_i}^{x_{i+1}}](BFF4C3CDB7D7BBBB40BFF4C3CDC0D1CAAC40A4BDA4CE3240A5B7A5F3A5D7A5BDA5F3CBA1_eq0020.gif)
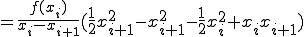
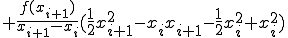
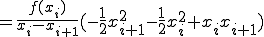
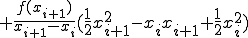
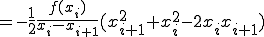
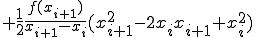
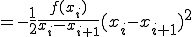
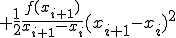
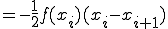
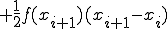
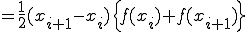 (1-5)
(1-5)
ここで、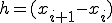
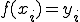
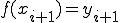
とおくと
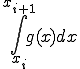
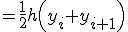 (1-6)
(1-6)
となる。
これを一区間ではなく、区間[a,b]にまで拡張します。
すると区間[a,b]を等間隔にn分割すると、
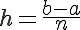
ここで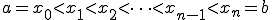
区間![[x_0,x_{1}] [x_0,x_{1}]](BFF4C3CDB7D7BBBB40BFF4C3CDC0D1CAAC40A4BDA4CE3240A5B7A5F3A5D7A5BDA5F3CBA1_eq0039.gif) ,
,![[x_1,x_{2}] [x_1,x_{2}]](BFF4C3CDB7D7BBBB40BFF4C3CDC0D1CAAC40A4BDA4CE3240A5B7A5F3A5D7A5BDA5F3CBA1_eq0040.gif) ,
,![[x_2,x_{3}] [x_2,x_{3}]](BFF4C3CDB7D7BBBB40BFF4C3CDC0D1CAAC40A4BDA4CE3240A5B7A5F3A5D7A5BDA5F3CBA1_eq0041.gif) ,
, ,
,![[x_{n-1},x_{n}] [x_{n-1},x_{n}]](BFF4C3CDB7D7BBBB40BFF4C3CDC0D1CAAC40A4BDA4CE3240A5B7A5F3A5D7A5BDA5F3CBA1_eq0043.gif)
の各微小台形の面積の総和は、
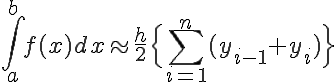
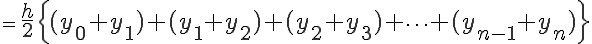
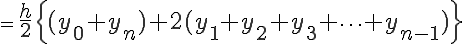 (1-7)
(1-7)
となります。

3点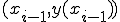 ,
, 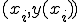 ,
,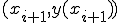
を通る直線を考える。
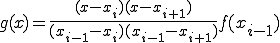
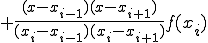
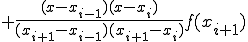
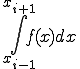
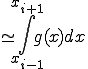
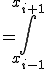
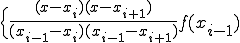
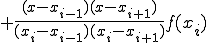
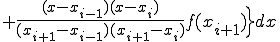
この直線の方程式は、以下となる。
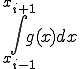
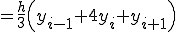 (2-1)
(2-1)
ただし、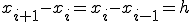
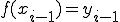
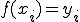
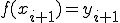
これを一区間ではなく、区間[a,b]にまで拡張します。
台形法では、区間の距離を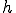 としましたが、
としましたが、
シンプソン法の場合は、区間の距離は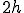 となります。すると区間[a,b]をn回の積分で行うとすると、
となります。すると区間[a,b]をn回の積分で行うとすると、
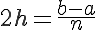
となるので、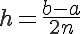
また、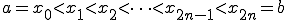
つまり、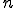 回の計算においてxの数は
回の計算においてxの数は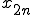 個となります。
個となります。
区間![[x_0,x_{1},x{2}] [x_0,x_{1},x{2}]](BFF4C3CDB7D7BBBB40BFF4C3CDC0D1CAAC40A4BDA4CE3240A5B7A5F3A5D7A5BDA5F3CBA1_eq0072.gif) ,
,![[x_{2},x_{3},x_{4}] [x_{2},x_{3},x_{4}]](BFF4C3CDB7D7BBBB40BFF4C3CDC0D1CAAC40A4BDA4CE3240A5B7A5F3A5D7A5BDA5F3CBA1_eq0073.gif) ,
,![[x_{4},x_{5},x_{6}] [x_{4},x_{5},x_{6}]](BFF4C3CDB7D7BBBB40BFF4C3CDC0D1CAAC40A4BDA4CE3240A5B7A5F3A5D7A5BDA5F3CBA1_eq0074.gif) ,
, ,
,![[x_{2n-2},x_{2n-1},x_{2n}] [x_{2n-2},x_{2n-1},x_{2n}]](BFF4C3CDB7D7BBBB40BFF4C3CDC0D1CAAC40A4BDA4CE3240A5B7A5F3A5D7A5BDA5F3CBA1_eq0076.gif)
の各微小台形の面積の総和は、
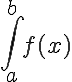
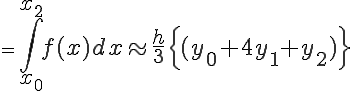
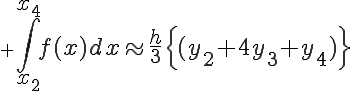
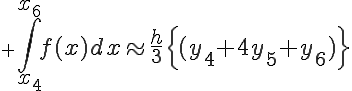
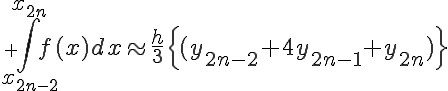
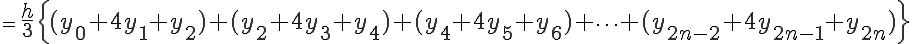
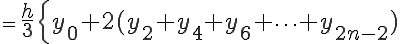
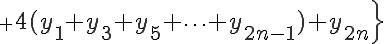
となります。
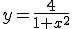 を区間
を区間![[0,1] [0,1]](BFF4C3CDB7D7BBBB40BFF4C3CDC0D1CAAC40A4BDA4CE3240A5B7A5F3A5D7A5BDA5F3CBA1_eq0088.gif) においてシンプソン法と台形法を用いて解け。
においてシンプソン法と台形法を用いて解け。
// suuti_sekibun.cpp : コンソール アプリケーションのエントリ ポイントを定義します。
//
#include "stdafx.h"
#include<iostream>
#include<fstream>
#include<io.h>
double sympson_method(double (*function)(double x),double a,double b,int num);
double daikei_method(double (*function)(double x),double a,double b,int num);
double func(double x);
int _tmain(int argc, _TCHAR* argv[])
{
errno_t err;
FILE *fp_output;
double ans_sympson=0.;
double ans_daikei=0.;
if( err = fopen_s(&fp_output,"simpsonAndDaikei_sekibun.txt","w") != 0){ exit(2);}
double a=0.;
double b=1.0;
//分割数を1から200まで分割する
for(int n=1;n<=200;n++){
double h2 = (b-a)/(double)n;
double h=h2/2.;
ans_daikei = daikei_method(&func,a,b,n);
ans_sympson = sympson_method(&func,a,b,n);
fprintf_s(fp_output,"%f %f %f\n",h,ans_daikei,ans_sympson);
}
if(fp_output != NULL) fclose(fp_output);
//getchar();
return 0;
}
//積分の範囲[a,b]とその範囲の分割数num
double sympson_method(double (*function)(double x),double a,double b,int num){
//積分の範囲とその範囲を分割する数numから求められる離散間隔
double h=0.;
double h2=0.;
//シンプソン法で使われる変数
double ans=0;
double term1=0.;
double term2=0.;
double term3=0.;
double term4=0.;
h2 = (b-a)/(double)num;
h=h2/2.;
ans=0.;
term1=0.;
term2=0.;
term3=0.;
term4=0.;
///// ここからsympson法 ///////////////
//第1項の計算
term1=(*function)(a);
//第2項の計算 y2+y4+y6+.....+y_{2n-2}
for(int i=2;i<=(2*num-2);i=i+2){
term2=term2+(*function)(a+i*h);
}
//第3項の計算 y1+y3+y5+....+y_{2n-1}
for(int i=1;i<=(2*num-1);i=i+2){
term3=term3+(*function)(a+i*h);
}
//第4項の計算
term4=(*function)(b);
ans=h/3.*(term1+2*term2+4*term3+term4);
return ans;
}
//積分の範囲[a,b]とその範囲の分割数num
double daikei_method(double (*function)(double x),double a,double b,int num){
double h = (b-a)/(float)num;
float ans=0;
for(int i=1;i<=num;i++){
ans=ans+(*function)(a+(i-1)*h)+(*function)(a+(i*h)) ;
}
return ans=h/2.*ans;
}
double func(double x){
double y;
y=4.0/(1.0+x*x);
return y;
}
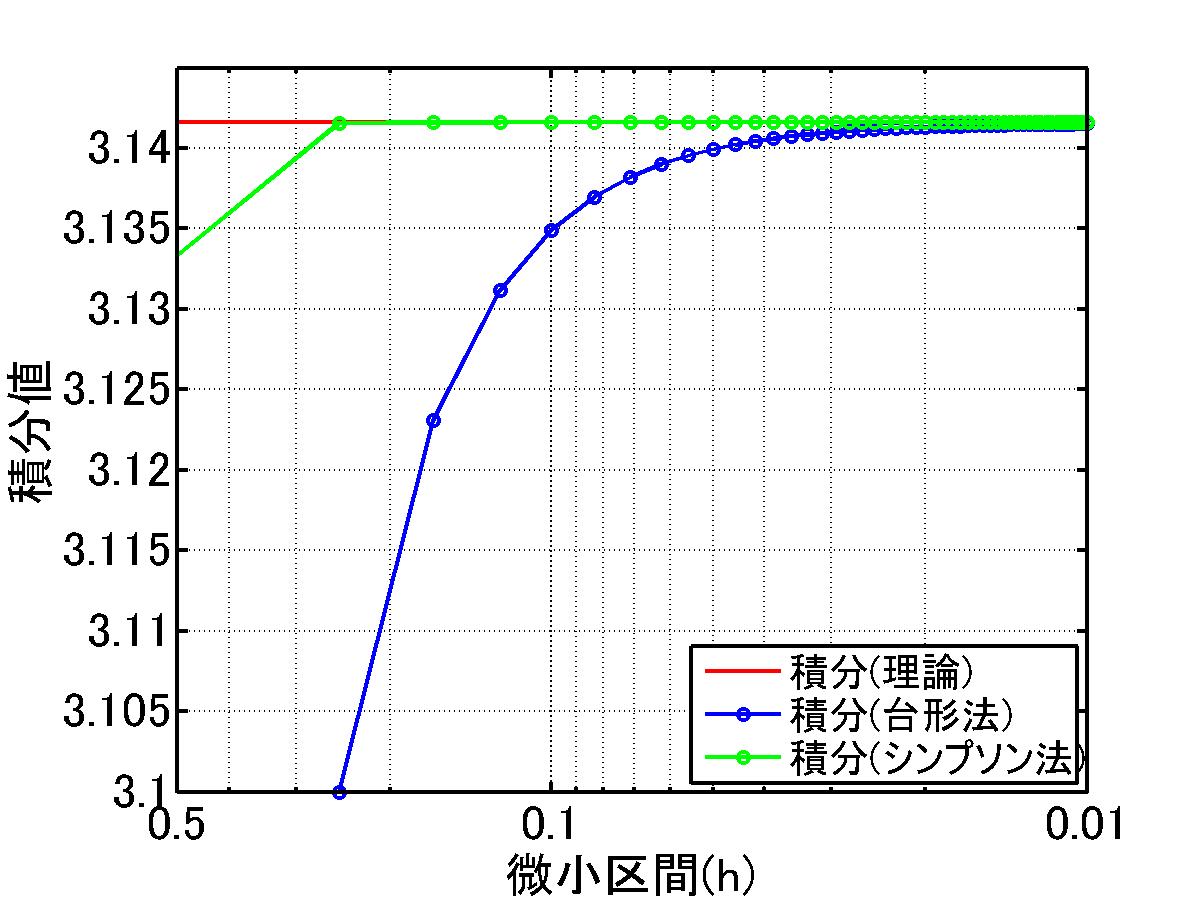
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% シンプソン法
%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
echo off
clear all
close all
load 'simpsonAndDaikei_sekibun.txt'
hi=simpsonAndDaikei_sekibun(:,1);
iti=ones(size(hi));
sekibun_real=iti.*3.14159;
daikei=simpsonAndDaikei_sekibun(:,2);
simpson=simpsonAndDaikei_sekibun(:,3);
semilogx(hi,sekibun_real,'r-','linewidth',2);
hold on
semilogx(hi,daikei,'bo-','linewidth',2);
hold on
semilogx(hi,simpson,'go-','linewidth',2);
hold on
grid on
%x軸を逆にする
set(gca,'XDir','reverse');
set(gca,'XTick',[0.01 0.1 0.5])
set(gca,'XTickLabel',{'0.01','0.1','0.5'})
xlabel('微小区間(h)','Fontsize',18)
ylabel('積分値','Fontsize',18)
h=legend('積分(理論)',...,
'積分(台形法)',...,
'積分(シンプソン法)',...,
4);
set(h,'FontSize',15)
axis([0.01 0.5 3.100 3.145]);
h=gca
get(h)
set(h,'LineWidth',2,...,
'FontSize',18)
print -djpeg suuti_sekibun_simpson_daikei.jpg