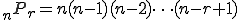
3 x 2 を考える。
3 x 2 とは3つの要素があり、それぞれの要素は2つの要素を持っていると考えられる。
つまり、行列である。
data[3][2]
[0] [1]
data[0] * *
data[1] * *
data[2] * *
つまり6個の要素を持つ。
void test(int* array){
//printf("array[0][1]=%x\n",array[0][1]); <--こんなことはできない
for(int i=0;i<6;i++){
printf("array=0x%x\n",array);
printf("*array=%x\n",*array);
array++;
}
}
int main(void){
int* matrixp;
int matrix[3][2]={{1,2},{3,4},{5,6}};
matrixp = (int *)matrix;
test(matrixp);
return 0;
}
array=0x12ff64 *array=1 array=0x12ff68 *array=2 array=0x12ff6c *array=3 array=0x12ff70 *array=4 array=0x12ff74 *array=5 array=0x12ff78 *array=6 Press any key to continue
データは0x12ff64番地から順々に並ぶため、ポインタの受け手側は、[2][3]か[3][2]か分からない。
異なるn個のものからr個取り出して1列に並べたものを、
n個からr個とる順列
といい、その総数は、
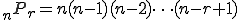
たとえば 6個の文字 a,b,c,d,e,fから3個の文字を取り出すとき、総数は
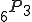
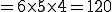
これを考える。
最初は 6通りから1つを選ぶ。
ひとつ選ぶと次は5通りから1つを選ぶ。
つまり
a b c d e f | | | | | | b c d e f a c d e f a b d e f a b c e f a b c d f a b c d e
6つの要素が各々5つの要素をもつことになるから
6 x 5 = 30
次に2つ選ぶと次は4通りから1つ選ぶから
a b c d e f | | | | | | b c d e f a c d e f a b d e f a b c e f a b c d f a b c d e | | | | | | | | | | c d e f b d e f b c e f b c d f b c d e 4 4 4 4 4
5つの要素はそれぞれ4つの要素をもつことになるから
6 x 5 x 4 = 120
となる。
nの階乗 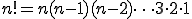
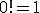
順列は、
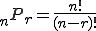
とくに 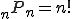
また、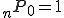
順列は、異なるn個のものからr個を取り出したとき!
組合せとは、異なるn個のものからr個取り出して1組にしたものを
n個からr個とる組合せといい、その総数は、
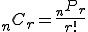
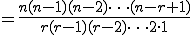
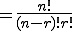
(1)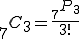
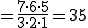
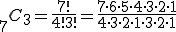
(2)7人から3人を選ぶ組合せ
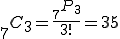 通り
通り
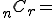
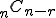
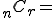
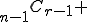
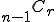
(i) 5人から2人の委員を選ぶ組合せは、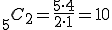
(i) 5人から委員にならない3人を選ぶ組合せは、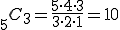
ゆえに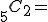
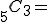
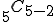
2項定理(binomial theorem)とは、2項式 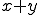 のべき乗(冪乗)
のべき乗(冪乗) 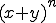 の展開(二項展開)
の展開(二項展開)
を表す公式のことである。
2項展開の一般項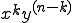 の係数を二項係数と呼び、
の係数を二項係数と呼び、
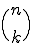
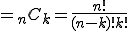
と表す。
すなわち2項定理は、
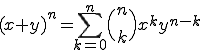
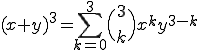
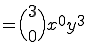
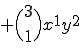
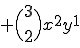
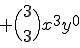
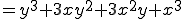
%メインファンクションの定義 function [C]=bincoeff(n); %2項係数: nCk = n! / k!(n-k)! %初期化 C=[]; %2項係数の計算 for k=0:n num = kai(n)/(kai(k)*kai(n-k)); C = [C,num]; end %サブファンクションの定義 function out = kai(x) %階乗 x! out=prod(1:x);
■結果
>> bincoeff(3)
ans =
1 3 3 1
Focus Up 数学 I + A 高橋陽一朗著 啓林館