(1)「ディジタル信号処理技術」玉井徳みち、長島厚、藤田泰弘、若井修造著 日経BP社
(2)「ディジタル信号処理の基礎」三上直樹著 CQ出版
(3)「C言語によるディジタル信号処理入門」三上直樹著 CQ出版
(4)「アナログ&ディジタルフィルタ入門」小野浩司著 日刊工業
(5)「フーリエの冒険」ヒッポファミリークラブ

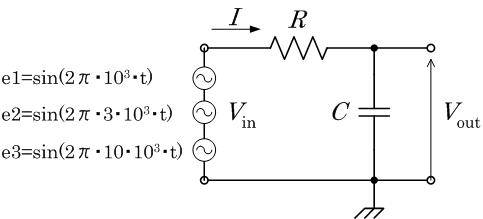
上記のような1次ローパスフィルタ(CR回路)は
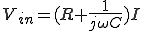 (1)
(1)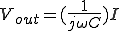 (2)
(2)
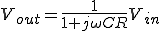 (3)
(3)
ここで、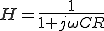 (4)
(4)
とすると
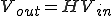 (5)
(5)

この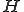 を伝達関数と呼ぶ。
を伝達関数と呼ぶ。
入力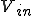 を
を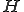 に印加したら出力
に印加したら出力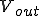 を得るという意味となる。
を得るという意味となる。
いま周波数を強調するために(5)式は、
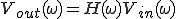 (6)
(6)
とおかれる。
「周波数領域の掛け算」は、「時間領域の畳み込み」なので、
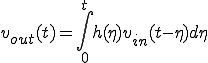 (7)
(7)
ここで、
 は入力
は入力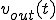 は出力
は出力 はフィルタ係数(インパルス応答)である。
はフィルタ係数(インパルス応答)である。
基本的にアナログ領域では、時間領域の処理は構成した回路
(この場合は、R,C素子で構成された回路)が行うので
周波数特性を知っていれば良い。
ディジタルフィルタは時間領域の畳み込みによって表現できる。
![x[n] x[n]](A5C7A5A3A5B8A5BFA5EBA5D5A5A3A5EBA5BFA4CEB4F0C1C3_eq0015.gif) は入力
は入力![y[n] y[n]](A5C7A5A3A5B8A5BFA5EBA5D5A5A3A5EBA5BFA4CEB4F0C1C3_eq0016.gif) は出力
は出力![h[n] h[n]](A5C7A5A3A5B8A5BFA5EBA5D5A5A3A5EBA5BFA4CEB4F0C1C3_eq0017.gif) はインパルス応答(フィルタ係数)
はインパルス応答(フィルタ係数)
![y[n]= \sum_{k=0}^{N-1} (h[k] x[n-k]) y[n]= \sum_{k=0}^{N-1} (h[k] x[n-k])](A5C7A5A3A5B8A5BFA5EBA5D5A5A3A5EBA5BFA4CEB4F0C1C3_eq0018.gif) (8)
(8)
= ![h[0]x[n-0] + h[1]x[n-1] + h[2]x[n-3] + ... + h[N-1]x[n-(N-1)] h[0]x[n-0] + h[1]x[n-1] + h[2]x[n-3] + ... + h[N-1]x[n-(N-1)]](A5C7A5A3A5B8A5BFA5EBA5D5A5A3A5EBA5BFA4CEB4F0C1C3_eq0019.gif)
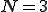 とすると、
とすると、![y[n]= \sum_{k=0}^{2} (h[k] x[n-k]) y[n]= \sum_{k=0}^{2} (h[k] x[n-k])](A5C7A5A3A5B8A5BFA5EBA5D5A5A3A5EBA5BFA4CEB4F0C1C3_eq0021.gif)
= ![h[0]x[n-0] + h[1]x[n-1] + h[2]x[n-3] h[0]x[n-0] + h[1]x[n-1] + h[2]x[n-3]](A5C7A5A3A5B8A5BFA5EBA5D5A5A3A5EBA5BFA4CEB4F0C1C3_eq0022.gif)
畳込みについてでも説明したが
畳み込みとは、「現在の状態を過去の積み重ね」で表現するということ。
x[n] は現在~ x[n-1]は現在からひとつ前の過去~ x[n-2]は現在からふたつ前の過去~
h[0]は現在の予想~ h[1]はひとつ先の予想~ h[2]はふたつ先の予想~
なので
![h[0]x[n-0] + h[1]x[n-1] + h[2]x[n-3] h[0]x[n-0] + h[1]x[n-1] + h[2]x[n-3]](A5C7A5A3A5B8A5BFA5EBA5D5A5A3A5EBA5BFA4CEB4F0C1C3_eq0023.gif)
は、
(現在@x[n]) x (現在の予想@h[0]) = "現在" + (ひとつ前の過去@x[n-1]) x (ひとつ過去からのひとつ未来の未来予想@h[1]) = ひとつ過去から予想される"現在" + (ふたつ前の過去@x[n-2]) x (ふたつ過去からのふたつ未来の未来予想@h[2]) = ふたつ過去から予想される"現在"
いま、
h(0)=0.8 h(1)=0.15 h(2)=0.05
とすると
y[n]=0.8*x[n] + 0.15*x[n-1] + 0.05*x[n-2]
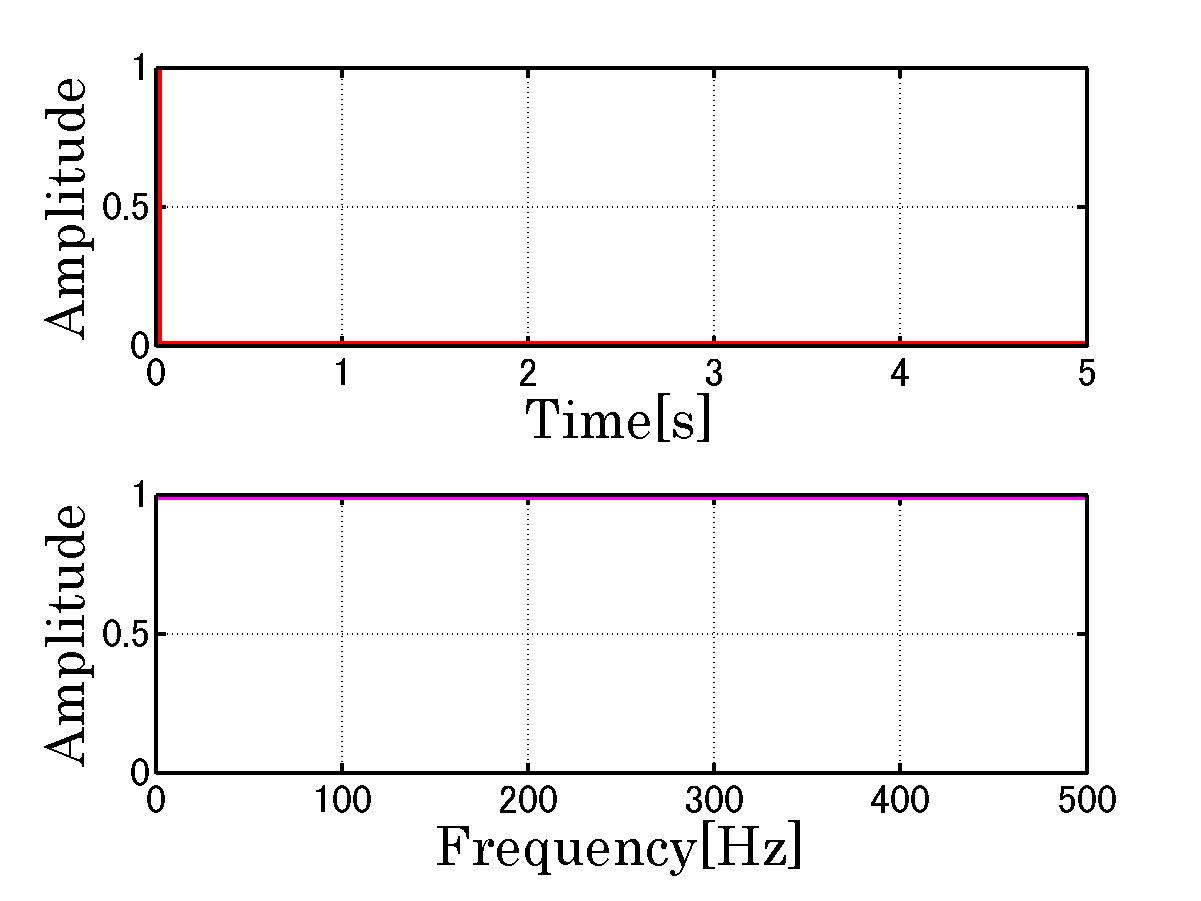
サンプリング周期 1 [ms] サンプリング周波数 1 [kHz] データ総数 5001 基本周波数 0.2[Hz]
インパルス信号とは、
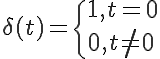 (9)
(9)
のような信号である。ディジタル信号では、
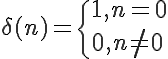 (10)
(10)
となる。
また
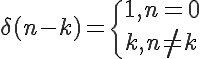
とかくとk遅れたインパルス信号を作ることができる。
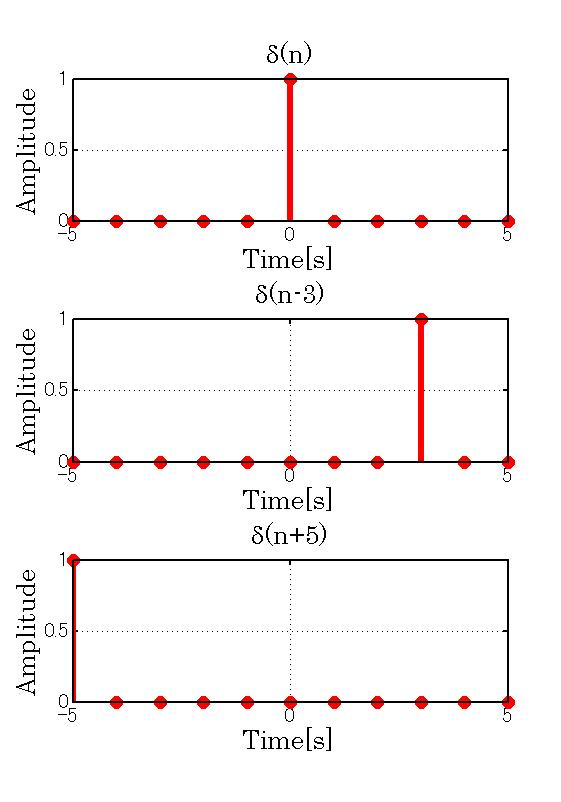
上図はさまざまなインパルス信号
インパルス応答とは、
インパルス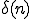 をフィルタへ入力したとき得られる出力信号
をフィルタへ入力したとき得られる出力信号
![y_{\delta}[n]= \sum_{k=0}^{N-1} (h[k] \delta[n-k]) y_{\delta}[n]= \sum_{k=0}^{N-1} (h[k] \delta[n-k])](A5C7A5A3A5B8A5BFA5EBA5D5A5A3A5EBA5BFA4CEB4F0C1C3_eq0028.gif) (11)
(11)
この ![y_{\delta}[n] y_{\delta}[n]](A5C7A5A3A5B8A5BFA5EBA5D5A5A3A5EBA5BFA4CEB4F0C1C3_eq0029.gif) がインパルス応答である。
がインパルス応答である。
ここで
インパルス信号が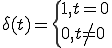
で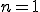

のときの(1)を求める。
![y_{\delta}[1] = \sum_{k=0}^{N-1} (h[k] \delta[1-k]) y_{\delta}[1] = \sum_{k=0}^{N-1} (h[k] \delta[1-k])](A5C7A5A3A5B8A5BFA5EBA5D5A5A3A5EBA5BFA4CEB4F0C1C3_eq0032.gif)
![=h[0]\delta[1-0] + h[1]\delta[1-1] + h[2]\delta[1-3] + ... + h[N-1]\delta[1-(N-1)] =h[0]\delta[1-0] + h[1]\delta[1-1] + h[2]\delta[1-3] + ... + h[N-1]\delta[1-(N-1)]](A5C7A5A3A5B8A5BFA5EBA5D5A5A3A5EBA5BFA4CEB4F0C1C3_eq0033.gif)
![=h[0]\delta[1] + h[1]\delta[0] + h[2]\delta[-2] + ... + h[N-1]\delta[2-N] =h[0]\delta[1] + h[1]\delta[0] + h[2]\delta[-2] + ... + h[N-1]\delta[2-N]](A5C7A5A3A5B8A5BFA5EBA5D5A5A3A5EBA5BFA4CEB4F0C1C3_eq0034.gif)
![=0 + h[1] + 0 + ... + 0 =0 + h[1] + 0 + ... + 0](A5C7A5A3A5B8A5BFA5EBA5D5A5A3A5EBA5BFA4CEB4F0C1C3_eq0035.gif)
![=h[1] =h[1]](A5C7A5A3A5B8A5BFA5EBA5D5A5A3A5EBA5BFA4CEB4F0C1C3_eq0036.gif)
ゆえに
![y_{\delta}[n] = h[n] y_{\delta}[n] = h[n]](A5C7A5A3A5B8A5BFA5EBA5D5A5A3A5EBA5BFA4CEB4F0C1C3_eq0037.gif) (12)
(12)
つまり、「インパルス応答とフィルタ係数は同じ」である。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% インパルス応答
% programming by embedded.samurai
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
echo off
clear all
close all
%サンプリング周期 1[ms]
dx=1e-3;
dfs=1/dx
% xの範囲は 0から0.001単位で5まで
x=[-5:1:5];
%データ総数
[gyo N]=size(x)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
subplot(3,1,1);
% インパルス信号を作る
y1=[zeros(5,1);1;zeros(N-6,1)]
stem(x,y1,'r-','linewidth',5);
% 文字の大きさ、線の太さの設定
set(gca,'LineWidth',2,...,
'FontSize',15);
xlabel('Time[s]','Fontsize',20,'FontName','Century');
ylabel('Amplitude','Fontsize',20,'FontName','Century');
title('\delta(n)','Fontsize',20,'FontName','Century');
% x-y範囲
axis([-5 5 -Inf Inf]);
grid on
hold on;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
subplot(3,1,2);
% インパルス信号を作る
y1=[zeros(8,1);1;zeros(N-9,1)]
stem(x,y1,'r-','linewidth',5);
% 文字の大きさ、線の太さの設定
set(gca,'LineWidth',2,...,
'FontSize',15);
xlabel('Time[s]','Fontsize',20,'FontName','Century');
ylabel('Amplitude','Fontsize',20,'FontName','Century');
title('\delta(n-3)','Fontsize',20,'FontName','Century');
% x-y範囲
axis([-5 5 -Inf Inf]);
grid on
hold on;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
subplot(3,1,3);
% インパルス信号を作る
y1=[1;zeros(N-1,1)]
stem(x,y1,'r-','linewidth',5);
% 文字の大きさ、線の太さの設定
set(gca,'LineWidth',2,...,
'FontSize',15);
xlabel('Time[s]','Fontsize',20,'FontName','Century');
ylabel('Amplitude','Fontsize',20,'FontName','Century');
title('\delta(n+5)','Fontsize',20,'FontName','Century');
% x-y範囲
axis([-5 5 -Inf Inf]);
grid on
hold on;
print -djpeg impulsu_outou_kakei.jpg