(1)「ディジタル信号処理技術」玉井徳みち、長島厚、藤田泰弘、若井修造著 日経BP社
(2)「ディジタル信号処理の基礎」三上直樹著 CQ出版
(3)「C言語によるディジタル信号処理入門」三上直樹著 CQ出版
(4)「アナログ&ディジタルフィルタ入門」小野浩司著 日刊工業
(5)「フーリエの冒険」ヒッポファミリークラブ
これから説明するフーリエ級数展開の式をまず示す。
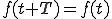
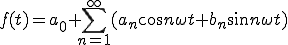
ここで、
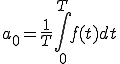
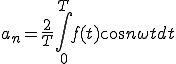
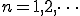
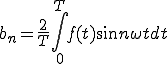
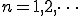
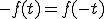 奇関数
奇関数
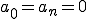
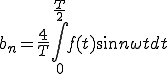
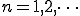
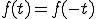 偶関数
偶関数
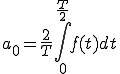
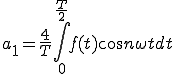
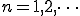
フーリエ級数展開を説明する前に、
突然ですが、例として「野菜ジュース」を考えてみます。
いま、トマト、セロリ、みかんがそれぞれ次図のように配合された
野菜ジュースがあるとします。
| トマト | 50% |
| セロリ | 30% |
| みかん | 20% |
| 計 | 100% |
|
50g |-------------------------- <---(トマト、セロリ、みかん入りジュース)
|
0g |------------------------- 時間
このように野菜ジュールはどの時間からみても容量50gのジュースで
時間軸上では、トマトとセロリとみかんがどのくらいの割りあいで入っているかを
調べることはできません。
*
* *
| * *
| * * *
| * * *
-----|------|-------|---------|-------|--- 成分
みかん ぶどう きゃべつ セロリ トマト
もし上のような成分軸に世界を変えられるならば、このように各野菜の成分が分かります。
同じように、波に対して上記のような思考で考えてみます。
結論から言いますと波というのは、
基本周波数の整数倍の周波数の波が足し合わさってできている
と考えることができます。
例として、のこぎり波で説明します。
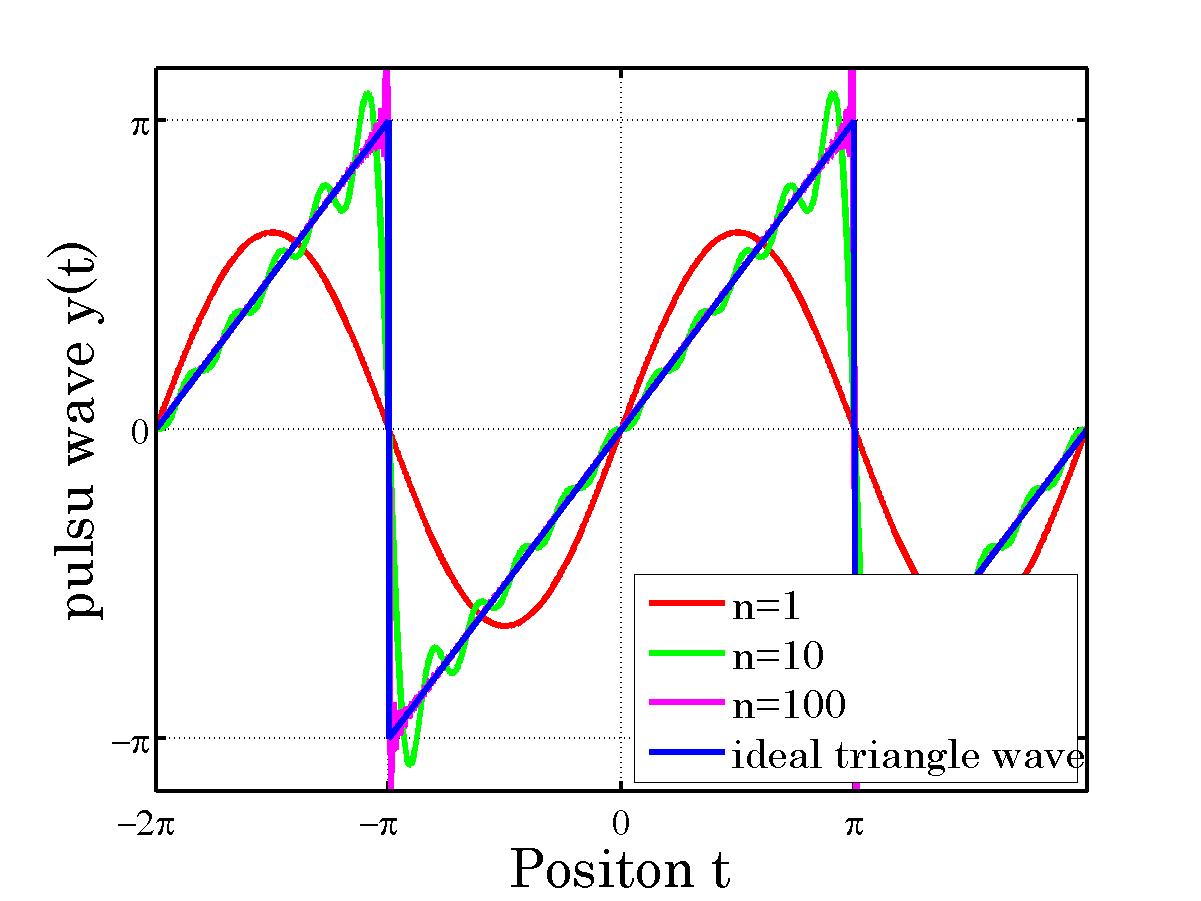
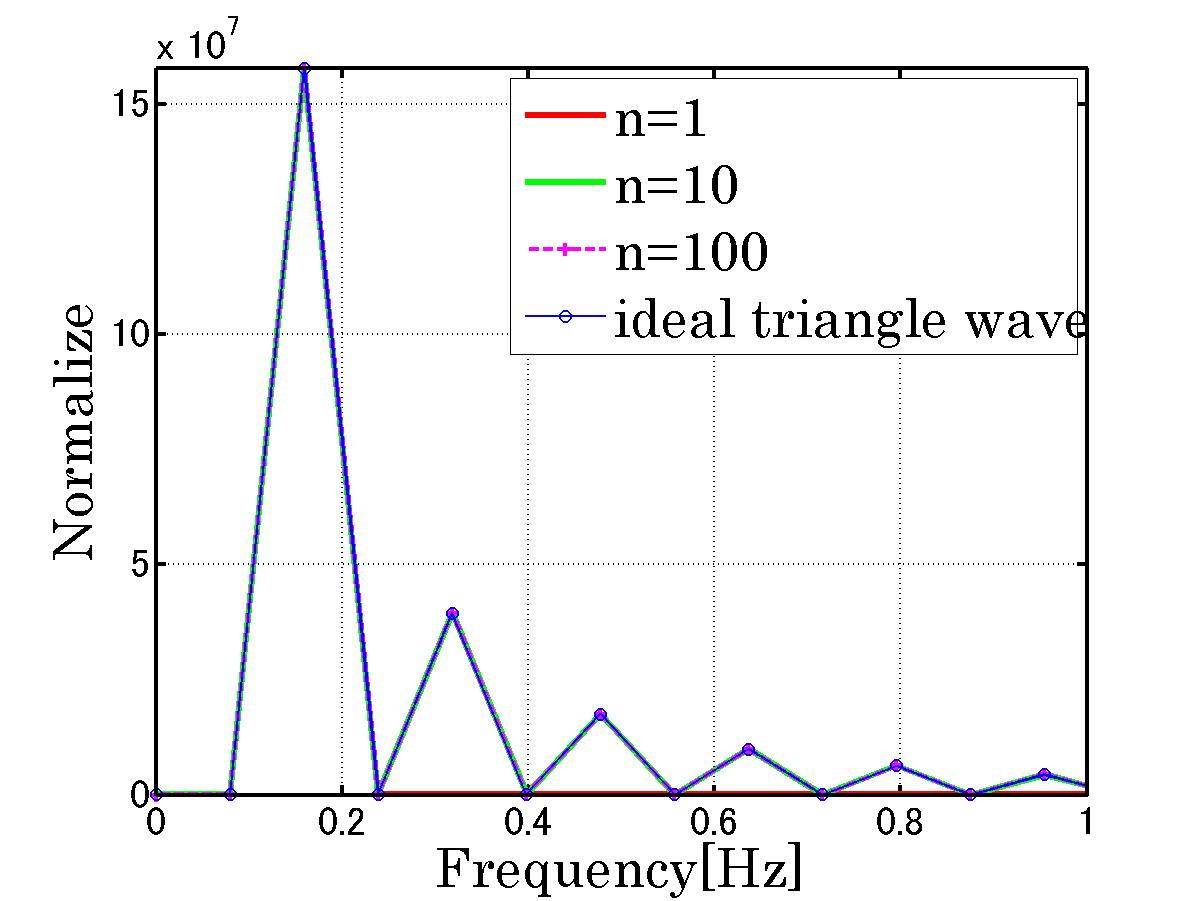
のこぎり波は、以下の式
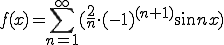
で表すことができます。
このとき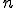 を
を
をグラフ化してみます。
図のようにに波を足し合わせればするほど三角波に近づいていきます。
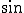 波と
波と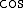 波
波
さて、波には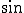 波と
波と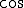 波があります。
波があります。
円を一周したときの
yの値をプロットすると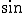 波を
波を
xの値をプロットすると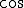 波を表すことができます。
波を表すことができます。
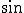 波も
波も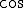 波も、円を一周すると(つまり360度になると)にもとの位置へ戻ります。
波も、円を一周すると(つまり360度になると)にもとの位置へ戻ります。
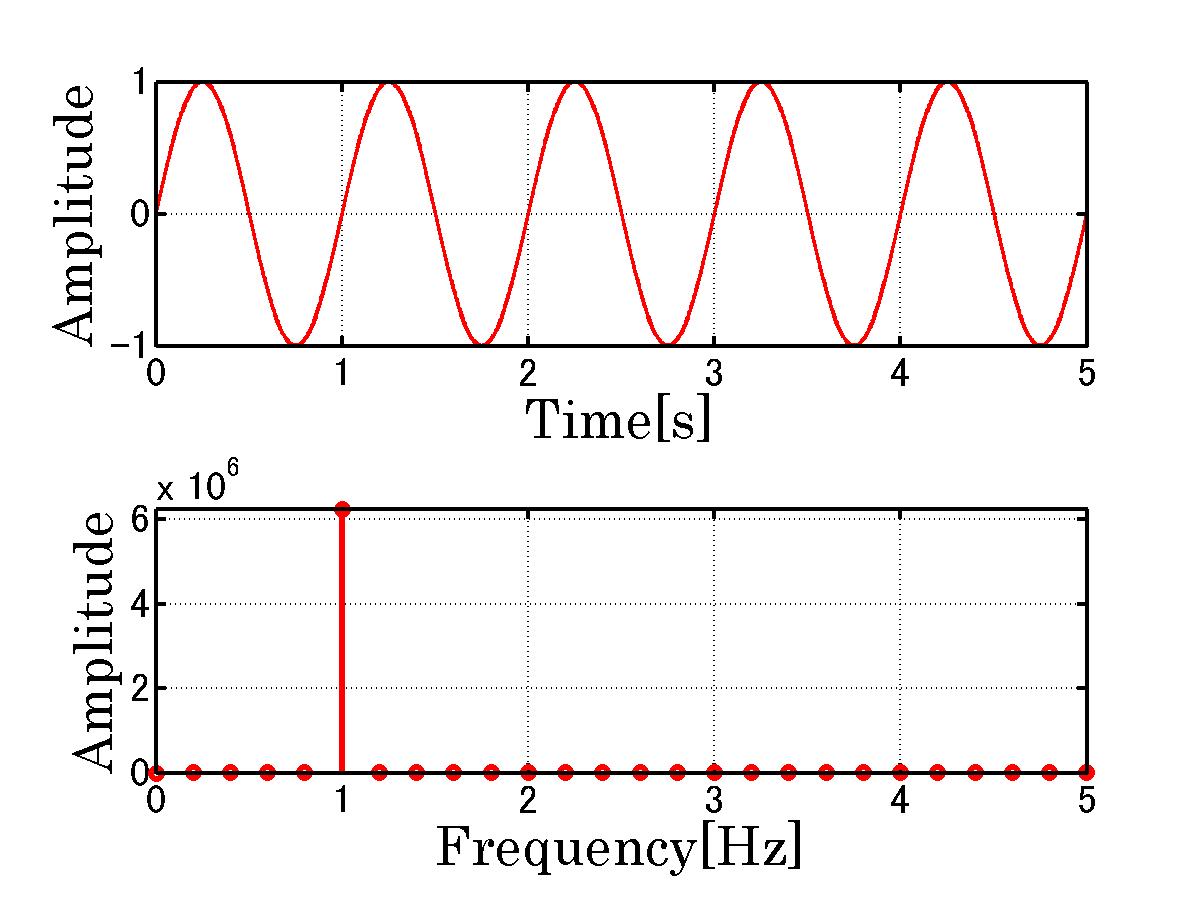
さて、正弦波は一周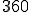 度(
度(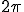 ラジアン)すると元に戻ります。
ラジアン)すると元に戻ります。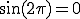
となるわけですね。
ここで横軸を時間として、時間が経過したときの正弦波を式で表してみます。
一周した時の時間を周期&mimetex(T)で表すと、
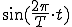 (1-1)
(1-1)
と表すことができます。
つまり![t=T[s] t=T[s]](A5D5A1BCA5EAA5A8B5E9BFF4C5B8B3AB_eq0030.gif) になると一周して元の位置に戻るわけですね。
になると一周して元の位置に戻るわけですね。
さて、この一周期の逆数は
1秒間に何回一周したかを表す
ことが分かります。
これを周波数 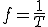 [Hz](1-2)といいます。
[Hz](1-2)といいます。
つまり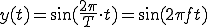 (1-3)
(1-3)
です。
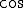 波(余弦波)というのは正弦波が
波(余弦波)というのは正弦波が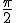 ずれた波形です。
ずれた波形です。
確かめてください。
余弦波が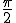 ずれた波形は正弦波です。
ずれた波形は正弦波です。
確かめてください。
先ほど、円を回転させて
ある位置の
縦軸をプロットすると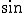 波に
波に
横軸をプロットすると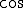 波が
波が
書けました。
円の半径が各々の波形の振幅になります。
そして、波の位置は、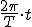 (1-4)
(1-4)
または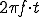 (1-5)
(1-5)
から求められます。
距離を求めるときには、速度に時間をかけましたよね。
つまり速度というのは、その物体のかけっこの性質を表していました。
かけっこが速い、遅いのを速度で定義するとみんなが納得できるわけです。
同じように波の性質は(1-4),(1-5)で定義できるわけです。
この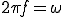 (1-6)
(1-6)
と定義した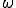 を角速度と定義してます。
を角速度と定義してます。
つまり、波の性質は角速度の違いで表現できるのです。
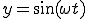 (1-7)
(1-7)
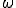 が違うと波の性質が違うというわけですね。
が違うと波の性質が違うというわけですね。
性質というのは味覚で言えば「甘い」「しょっぱい」「辛い」と同じようなものと考えてかまいません。
しかしながら甘いものとしょっぱいものを容器に入れたとして
甘いものの量が多ければ全体の味覚は甘く感じるし、しょっぱいものを入れればしょっぱく感じる。
それを表すのが先ほどの円の半径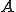
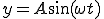 (1-8)
(1-8)
のAつまり振幅が量を表しているのです。
ある任意の波は、性質を現す角速度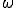 の整数倍の集まりで表現できます。
の整数倍の集まりで表現できます。
その性質がない波形は、振幅0として消えます。
ですので、各々の波の振幅(量)を求めることで、以下のような形
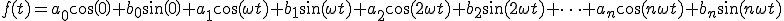
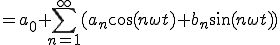
で複雑な波を表すことができます。
では複雑な波を構成する各々の波の振幅はどう求めるのでしょうか?
次からそれを説明します。
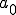 を求める
を求める
次に複雑な波から一つ一つの波の振幅(量)を取り出す操作をやってみます。
つまり複雑な波を個々の波に分ける作業です。
まず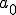 を考えてみる。
を考えてみる。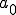 は波が0からどの位上にあるか
は波が0からどの位上にあるか
つまりバイアス電圧のようなものと考えてもらってかまわない。
その他の波はバイアスを中心にして上下に揺れている。つまり1周期分の面積は0になる。
つまり複雑な波の1周期分の面積を求めれば図のように赤の面積部位だけが残る。
後は、それを1周期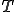 で割れば
で割れば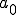 を求めることができます。
を求めることができます。
つまり
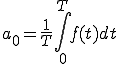 (2-1)
(2-1)
となります。
この式は、
「a0は複雑な波f(t)の一周期(0からT)までの面積を求めてTで割る」
という意味です。
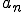
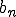 を求める
を求める
波は上下に揺れているので同じ周波数の波を掛けてやればマイナスの部分がプラスになる。
図の青線のように。青線をよく眺めれば
青線が0の基準線との間に作る面積は
0〜T/2までの長方形の面積に等しくなることが波形の対称性より明らかである。
つまりanを求めたいならば求めたい正弦波と同じ周波数の正弦波を掛けて
マイナス成分を消しそれの1周期分の面積を求めると
を掛け合わせた長方形となる。
求めたい周波数の信号以外は、マイナスとプラスの成分が残り打ち消しあって面積0となる。
つまり
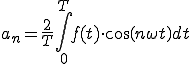
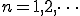 (2-2)
(2-2)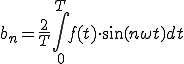
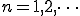 (2-3)
(2-3)
となる。
この式の意味は、
a_n は、複雑な波f(t)に求めたい波cos(nwt)をかけて、0からTまでの面積を求めてT/2で割る。
b_n は、複雑な波f(t)に求めたい波sin(nwt)をかけて、0からTまでの面積を求めてT/2で割る。
という意味です。
つまり、複雑な波を構成する各々の波の量を求めるわけです。
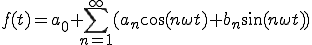
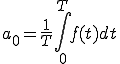 (2-1)
(2-1)
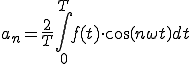
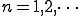 (2-2)
(2-2)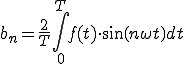
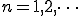 (2-3)
(2-3)


のこぎり波は、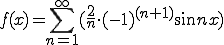
のように表される。
この式を求める。
■問い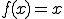 を
を 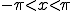 なる区間でフーリエ展開する。
なる区間でフーリエ展開する。
■解答
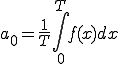
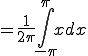
![= \frac{1}{2\pi}\Big[\frac{x^2}{2}\Big]^{\pi}_{-\pi} = \frac{1}{2\pi}\Big[\frac{x^2}{2}\Big]^{\pi}_{-\pi}](A5D5A1BCA5EAA5A8B5E9BFF4C5B8B3AB_eq0072.gif)
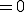
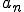 は
は
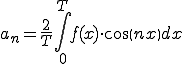
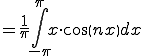
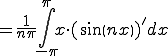
![= \frac{1}{n\pi}\Big{ \[ x\sin(n x) \]^{\pi}_{-\pi} -\int^{\pi}_{-\pi} \sin(nx) dx \Big} = \frac{1}{n\pi}\Big{ \[ x\sin(n x) \]^{\pi}_{-\pi} -\int^{\pi}_{-\pi} \sin(nx) dx \Big}](A5D5A1BCA5EAA5A8B5E9BFF4C5B8B3AB_eq0078.gif)
![= \frac{1}{n\pi}\[ \frac{1}{n}\cos(n x) \]^{\pi}_{-\pi} = \frac{1}{n\pi}\[ \frac{1}{n}\cos(n x) \]^{\pi}_{-\pi}](A5D5A1BCA5EAA5A8B5E9BFF4C5B8B3AB_eq0079.gif)
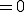
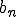 は
は
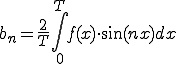
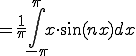
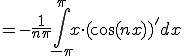
![= -\frac{1}{n\pi}\Big{ \[ x\cos(n x) \]^{\pi}_{-\pi} -\int^{\pi}_{-\pi} \cos(nx) dx \Big} = -\frac{1}{n\pi}\Big{ \[ x\cos(n x) \]^{\pi}_{-\pi} -\int^{\pi}_{-\pi} \cos(nx) dx \Big}](A5D5A1BCA5EAA5A8B5E9BFF4C5B8B3AB_eq0085.gif)
![= -\frac{1}{n\pi}\[ x\cos(n x) \]^{\pi}_{-\pi} -\[\frac{1}{n}\sin(nx)\]^{\pi}_{-\pi} = -\frac{1}{n\pi}\[ x\cos(n x) \]^{\pi}_{-\pi} -\[\frac{1}{n}\sin(nx)\]^{\pi}_{-\pi}](A5D5A1BCA5EAA5A8B5E9BFF4C5B8B3AB_eq0086.gif)
![= -\frac{1}{n\pi}\[ \pi\cos(n \pi) - (-\pi)\cos(n(-\pi)) \] = -\frac{1}{n\pi}\[ \pi\cos(n \pi) - (-\pi)\cos(n(-\pi)) \]](A5D5A1BCA5EAA5A8B5E9BFF4C5B8B3AB_eq0087.gif)
![= -\frac{1}{n\pi}\[ 2\pi\cos(n \pi) \] = -\frac{1}{n\pi}\[ 2\pi\cos(n \pi) \]](A5D5A1BCA5EAA5A8B5E9BFF4C5B8B3AB_eq0088.gif)
![= -\frac{2}{n}\[ \cos(n \pi) \] = -\frac{2}{n}\[ \cos(n \pi) \]](A5D5A1BCA5EAA5A8B5E9BFF4C5B8B3AB_eq0089.gif)
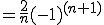
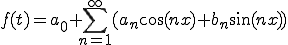
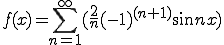
となる。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 三角波形を表示
% programming by embedded.samurai
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
echo off
clear all
close all
%サンプリング周期 1[ms]
dx=1e-3;
% xの範囲は -pi/2から0.001単位で3piまで
x=[-2*pi:dx:2*pi];
xx = x/pi;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% n=1のとき
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
figure(1);
y1=0;
for m=1:1:1
y=(2/m)*(-1)^(m+1)*sin(m.*x);
y1=y1+y;
end
y1
plot(xx,y1/pi,'r-','linewidth',3);
hold on;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% n=10のとき
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
y2=0;
for m=1:1:10
y=(2/m)*(-1)^(m+1)*sin(m.*x);
y2=y2+y;
end
plot(xx,y2/pi,'g-','linewidth',3);
hold on;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% n=100のとき
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
y3=0;
for m=1:1:100
y=(2/m)*(-1)^(m+1)*sin(m.*x);
y3=y3+y;
end
plot(xx,y3/pi,'m-','linewidth',3);
hold on;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 理想パルス
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
data=[];
for n=x
if ( n >= -2*pi) && ( n < -pi)
y=n +2*pi;
data=[data,y];
elseif (n >= -pi) && (n < pi)
y=n;
data=[data,y];
elseif (n >= pi) && (n <= 2*pi)
y=n -2*pi;
data=[data,y];
end
end
plot(xx,data/pi,'b-','linewidth',3);
hold on;
% xラベルとその文字の大きさ、線の太さの設定
str1={'-3p','-2p','-p','0','p','2p','3p'}
set(gca,'FontName','symbol','xtick',[-3:1:3],'xticklabel',str1)
str2={'-3p','-2p','-p','0','p','2p','3p'}
set(gca,'FontName','symbol','ytick',[-3:1:3],'yticklabel',str2)
set(gca,'LineWidth',2,'FontSize',18)
% x-y範囲
axis([-Inf Inf -Inf Inf]);
grid on
% xラベル、yラベル
xlabel('Positon t','Fontsize',20,'FontName','Century');
ylabel('pulsu wave y(t)','Fontsize',20,'FontName','Century')
% キャプション
h=legend('n=1',...,
'n=10',...,
'n=100',...,
'ideal triangle wave',...,
4);
set(h,'FontSize',15,'FontName','Century');
print -djpeg sankakuwave_t.jpg
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
figure(2);
%サンプリング周波数 1kHz
df=1/dx
%xの数 7854
[gyo retu]=size(x)
%基本周波数 0.1273[Hz]
bf=df/retu
%FFTの結果は複素数である
fftdata1 = fft(y1)';
fftdata2 = fft(y2)';
fftdata3 = fft(y3)';
fftdata4 = fft(data)';
%FFTの絶対値を求める
power1=abs(fftdata1).^2;
power2=abs(fftdata2).^2;
power3=abs(fftdata3).^2;
power4=abs(fftdata4).^2;
%離散周波数を作る
freq = [0:retu-1]'*bf
plot(freq,power1,'r-','linewidth',3);
hold on
plot(freq,power2,'g-','linewidth',3);
hold on
plot(freq,power3,'m+--','linewidth',2);
hold on
plot(freq,power4,'bo-','linewidth',1);
hold on
axis([0 1 0 Inf]);
set(gca,'LineWidth',2,...,
'FontSize',15);
xlabel('Frequency[Hz]','Fontsize',20,'FontName','Century');
ylabel('Normalize','Fontsize',20,'FontName','Century');
% キャプション
h=legend('n=1',...,
'n=10',...,
'n=100',...,
'ideal triangle wave',...,
1);
set(h,'FontSize',20,'FontName','Century');
grid on
print -djpeg sankakuwave_f.jpg