微分フィルタ

参考文献及びWEB

参考文献

(1)「例題で学ぶ過渡現象」大重力、森本義広、神田一伸　共著　森北出版
(2)「ディジタル信号処理技術」玉井徳みち、長島厚、藤田泰弘、若井修造著日経BP社
(3)「ディジタル信号処理の基礎」三上直樹著 CQ出版
(4)「C言語によるディジタル信号処理入門」三上直樹著 CQ出版
(5)「アナログ&ディジタルフィルタ入門」小野浩司著日刊工業
(6)「フーリエの冒険」ヒッポファミリークラブ
(7)「C言語ではじめる医用情報処理」小高和宏著　Ohmsha

あわせて読む

1次フィルタ
フーリエ級数展開
畳込みについて
時間領域と周波数領域
入力信号
平均@分散@標準偏差
移動平均

微分フィルタ-時間軸方向のデータの変化の様子を検出する

微分は差分

微分するためには、現在のデータから過去のデータを順々に引いていけばよい。

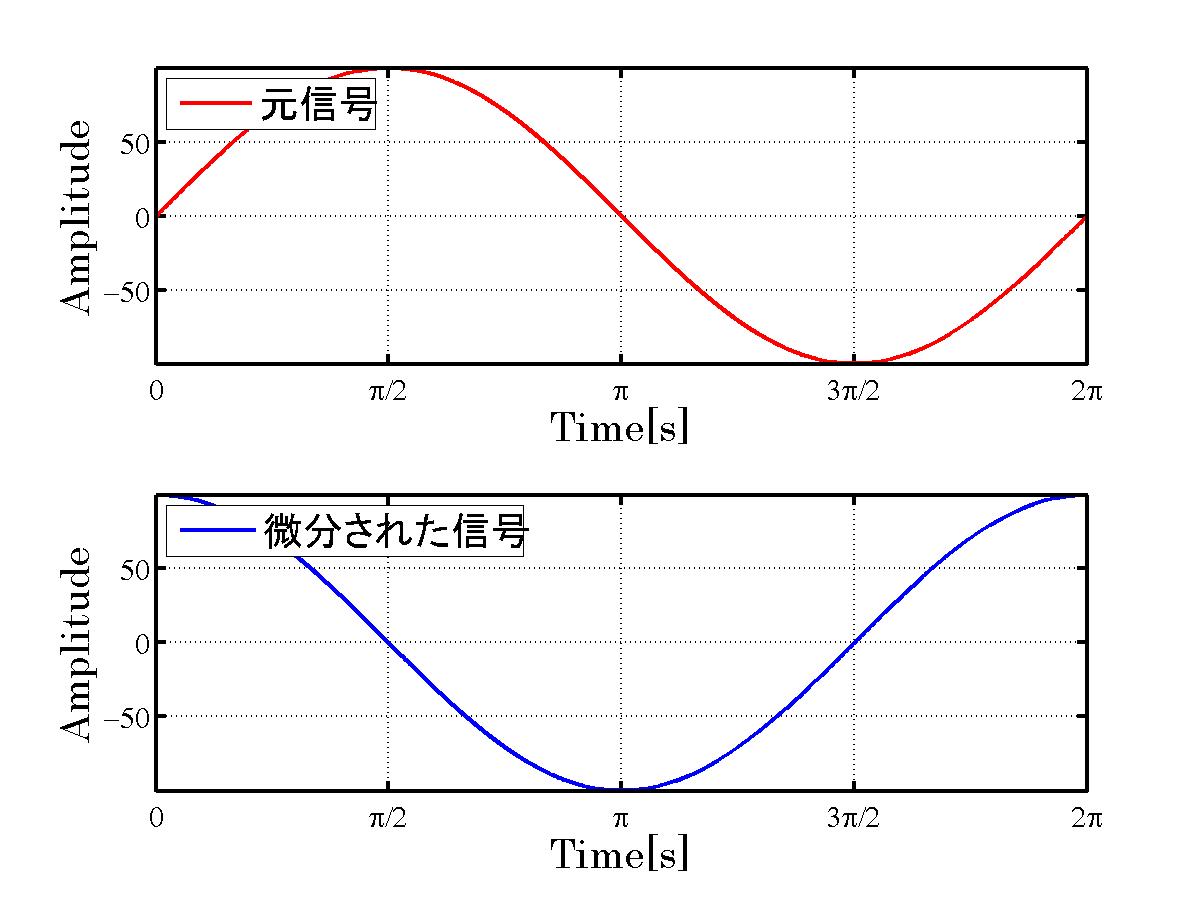
このようにsin信号は微分されてcos信号となっている。

微分フィルタは、変化をより強調する効果を持っています。

Matlabソース　bibun_filter.m

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% bibun filter sample program
%                 programming by embedded.samurai
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
echo off
clear all
close all

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 1[Hz]を表示
% ここはテスト
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
figure(1);

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
subplot(2,1,1)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

dt=0.001;
x=[0:dt:2*pi]
ty1=100*sin(x);
xx=x/pi;
plot(xx,ty1,'r-','linewidth',2);
grid on
hold on;

% xラベルとその文字の大きさ、線の太さの設定
str={'0','p/2','p','3p/2','2p'}
set(gca,'FontName','symbol','xtick',[0:.5:2],'xticklabel',str)
set(gca,'LineWidth',2,'FontSize',18)

h=gca;
set(h,'LineWidth',2,...,
'FontSize',15);

% キャプション
h=legend('元信号',...,
2);
set(h,'FontSize',15,'FontName','MS 明朝');

xlabel('Time[s]','Fontsize',15,'FontName','Century');
ylabel('Amplitude','Fontsize',15,'FontName','Century')

% x-y範囲
axis([0 2 -Inf Inf]); %2なのに注意！'xtick',[0:.5:2]

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
subplot(2,1,2) 
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

% 微分フィルタ
y=[];
[gyo retu]=size(ty1);

lastdata=ty1(1);

for i=[2:1:retu]
 indata=ty1(i);
 data=(indata-lastdata)/dt;
 y=[y,data];
 lastdata=indata;
end

plot(xx(2:retu),y,'b-','linewidth',2);
grid on;

% xラベルとその文字の大きさ、線の太さの設定
str={'0','p/2','p','3p/2','2p'}
set(gca,'FontName','symbol','xtick',[0:.5:2],'xticklabel',str)
set(gca,'LineWidth',2,'FontSize',18)

h=gca;
set(h,'LineWidth',2,...,
'FontSize',15);

% キャプション
h=legend('微分された信号',...,
2);
set(h,'FontSize',15,'FontName','MS 明朝');

xlabel('Time[s]','Fontsize',15,'FontName','Century');
ylabel('Amplitude','Fontsize',15,'FontName','Century')
 
% x-y範囲
axis([0 2 -Inf Inf]); %2なのに注意！'xtick',[0:.5:2]

print -djpeg bibun_filter.jpg

FFTで微分フィルタをしてみる

微分フィルタのフィルタ係数は、

h[0]=1, h[1]=-1

とみなすことができる。つまり

$h[n] = \delta[n]-\delta[n-1]$

そこで元信号とフィルタ係数を周波数領域に変換したのちかけあわせ、
フーリエ逆変換すると

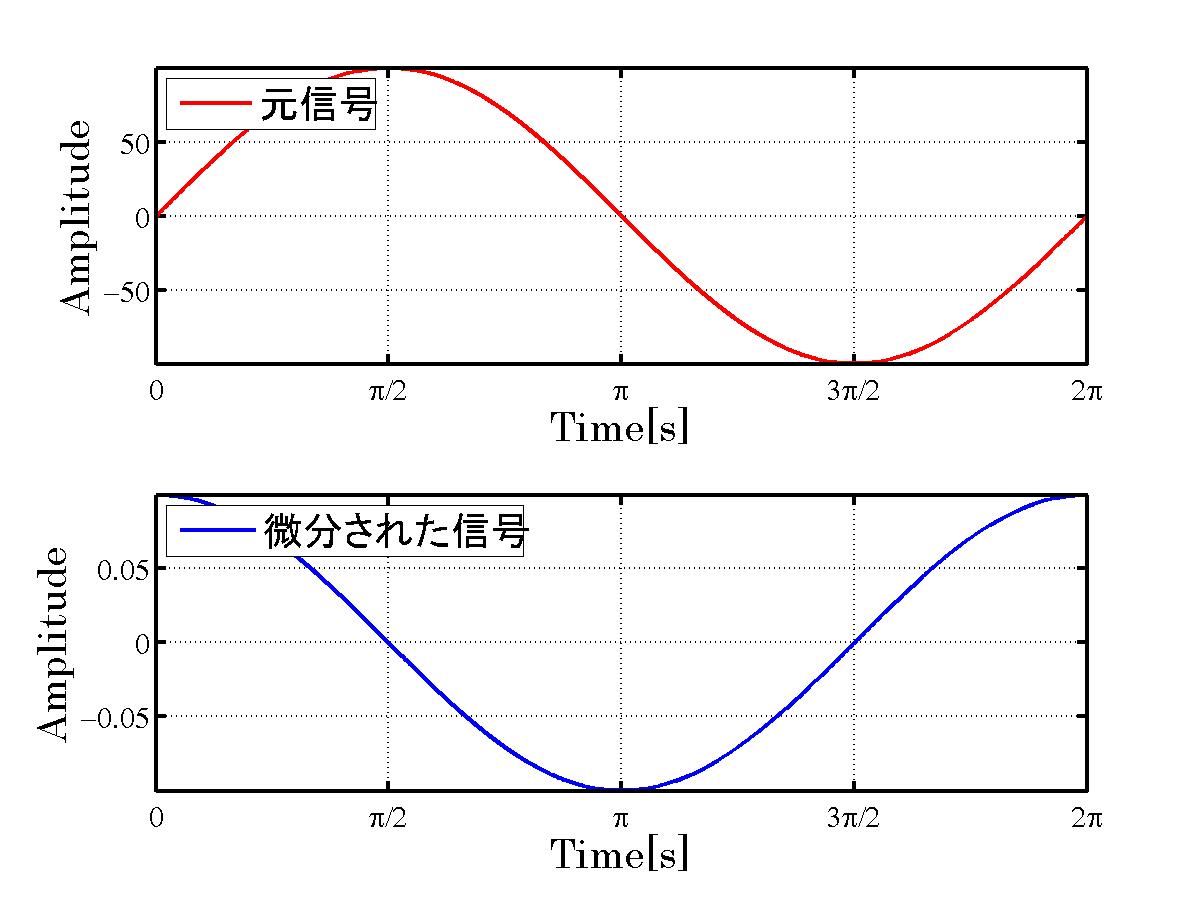
結果同じように正弦波は微分され、余弦波となる。

Matlabソース bibun_filter_fft.m

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% bibun filter fft sample program
%                 programming by embedded.samurai
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
echo off
clear all
close all

figure(1);

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
subplot(2,1,1)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

dt=0.001;
x=[0:dt:2*pi]
ty1=100*sin(x);
xx=x/pi;
plot(xx,ty1,'r-','linewidth',2);
grid on
hold on;

% xラベルとその文字の大きさ、線の太さの設定
str={'0','p/2','p','3p/2','2p'}
set(gca,'FontName','symbol','xtick',[0:.5:2],'xticklabel',str)
set(gca,'LineWidth',2,'FontSize',18)

h=gca;
set(h,'LineWidth',2,...,
'FontSize',15);

% キャプション
h=legend('元信号',...,
2);
set(h,'FontSize',15,'FontName','MS 明朝');

xlabel('Time[s]','Fontsize',15,'FontName','Century');
ylabel('Amplitude','Fontsize',15,'FontName','Century')

% x-y範囲
axis([0 2 -Inf Inf]); %2なのに注意！'xtick',[0:.5:2]

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
subplot(2,1,2)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

% 微分フィルタ
%元信号をフーリエ変換する
fftx=fft(ty1);
[gyo retu]=size(ty1)

hn=[1,-1];
ffthn=fft(hn,retu);
[gyo2 retu2]=size(ffthn)

yfft=fftx.*ffthn;

%逆フーリエ変換
yifft=ifft(yfft)

plot(xx,yifft,'b-','linewidth',2);
grid on;

% xラベルとその文字の大きさ、線の太さの設定
str={'0','p/2','p','3p/2','2p'}
set(gca,'FontName','symbol','xtick',[0:.5:2],'xticklabel',str)
set(gca,'LineWidth',2,'FontSize',18)

h=gca;
set(h,'LineWidth',2,...,
'FontSize',15);

% キャプション
h=legend('微分された信号',...,
2);
set(h,'FontSize',15,'FontName','MS 明朝');

xlabel('Time[s]','Fontsize',15,'FontName','Century');
ylabel('Amplitude','Fontsize',15,'FontName','Century')

% x-y範囲
axis([0 2 -Inf Inf]); %2なのに注意！'xtick',[0:.5:2]
 
print -djpeg bibun_filter_fft.jpg