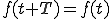
(1)「ディジタル信号処理技術」玉井徳みち、長島厚、藤田泰弘、若井修造著 日経BP社
(2)「ディジタル信号処理の基礎」三上直樹著 CQ出版
(3)「C言語によるディジタル信号処理入門」三上直樹著 CQ出版
(4)「アナログ&ディジタルフィルタ入門」小野浩司著 日刊工業
(5)「フーリエの冒険」ヒッポファミリークラブ
フーリエ級数展開の式はこうでした。
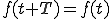
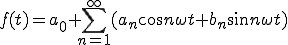
ここで、
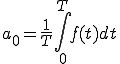
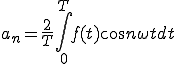
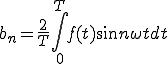
ベクトルは、方向と大きさを表す。
位置は関係ない。
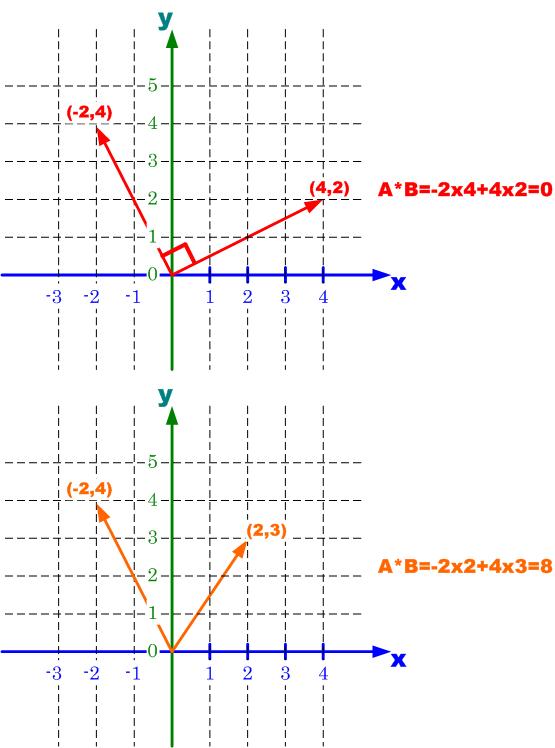
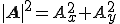
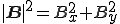
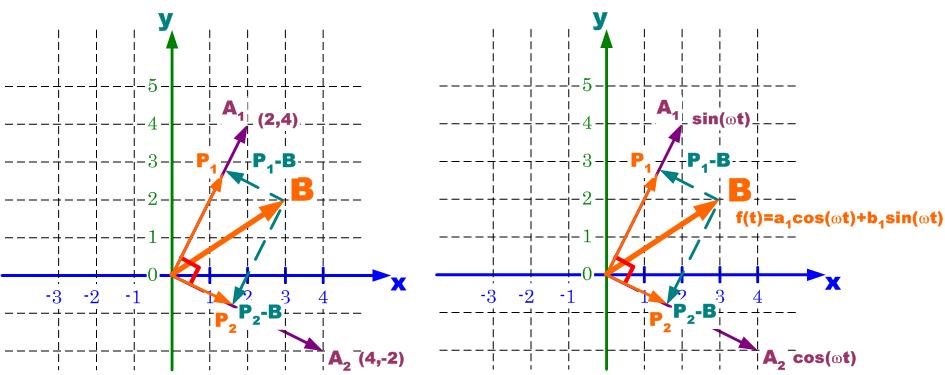
図1-1
波というものは各々の正弦波と余弦波の足し合わせで表現できることが分かりました。
ここでちょっと寄り道してみます。
図1-1を見てください。
今複雑な波を各々の成分の合成ということでベクトル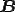 で表すことを考えてみます。
で表すことを考えてみます。
全体の波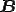 は各々の成分の波
は各々の成分の波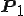 と
と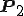 の合成によって
の合成によって
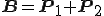
として表すことができます。
では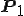 ,
,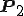 を
を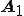 ,
,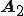 で表すにはどうしたら良いのでしょうか?
で表すにはどうしたら良いのでしょうか?
これには射影という考えかたを導入することで解決できます。
今ベクトル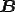 から
から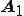 に垂線を下ろしますと紫の線は
に垂線を下ろしますと紫の線は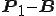 と表すことができます。
と表すことができます。
ここで内積を考えてみます。
内積は2つの直線が垂直かどうかを調べるときに使います。
ベクトル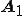 と
と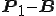 は垂直なので
は垂直なので
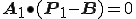
になります。
ところで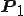 はベクトル
はベクトル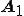 をx倍したものと考えることができますので
をx倍したものと考えることができますので
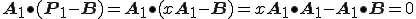
となりxは
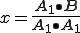
となる。これから
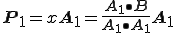
と成分を抽出することができます。
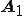 をsin波,
をsin波,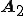 をcos波で表したベクトルとして
をcos波で表したベクトルとして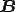 を表す
を表す

今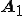 をsin波,
をsin波,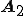 をcos波で表したベクトルとします。
をcos波で表したベクトルとします。
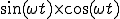 の一周期の総和を計算してみる
の一周期の総和を計算してみる
正弦波と余弦波をかけて一周期分の総和を取る
正弦波と余弦波をかけて一周期分の総和を取るプログラム
ここでは、
正弦波と余弦波の各々の要素をすべて足し合わせると0になることを確認します。
今、サンプリング時間0.004[s]で5[Hz]の正弦波と余弦波の一周期分の総和を求めます。
周波数5[Hz]は、周期0.2[s]ですので、1周期は、0.2/0.004=50点となり、
正弦波、余弦波は50個の要素で表されることが分かります。
いま、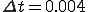 とし、
とし、
ベクトル にあたるものを
にあたるものを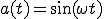
ベクトル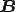 にあたるものを
にあたるものを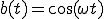
とします。
 のとき
のとき
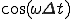
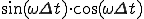 (2-1a)
(2-1a)
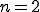 のとき
のとき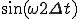
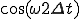
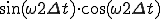 (2-1b)
(2-1b)
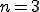 のとき
のとき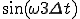 ~
~ 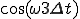
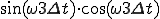 (2-1c)
(2-1c)
のように各々の要素同士をかけあわせ、それを足し算していきます。
(2-1a)+(2-1b)+(2-1c)+ ....
のようにです。
数式で表すと
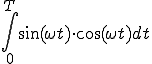 (2-2)
(2-2)
になります。
プログラムの結果をみると分かりますように(2番目のグラフの一周期後の緑のバー)
1周期足すと0になることが分かります。
各々の要素をかけて足す動作は、内積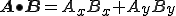
の動作と同じですので、(2-2)式は、
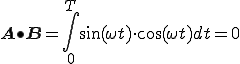 (2-3)
(2-3)
自分以外の波形との内積は全て0となります。
各自確かめてみてください。つまり全ての波はお互いに直交しています。
内積を取ることと積の積分は同じです。
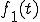 を求める
を求める

ここから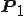 ,
,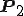 を求めて
を求めて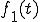 を求めてみます。
を求めてみます。
今フーリエ級数でいうところの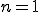 の時の
の時の
各成分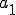 ,
,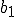 を求めてみようということです。
を求めてみようということです。
いまちょうど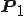 が
が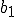 に当たると考えることができます。
に当たると考えることができます。
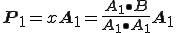
に代入すると
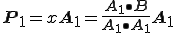
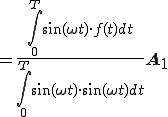
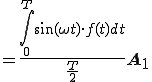
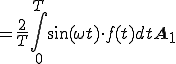
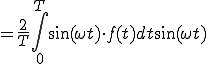
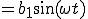 (2-4)
(2-4)
となり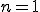 のときの
のときの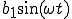 の式と同じになりました。
の式と同じになりました。
ここで
フーリエ級数展開における4式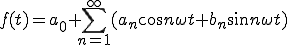 (1-1)
(1-1)
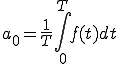 (1-2)
(1-2)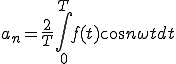
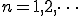 (1-3)
(1-3)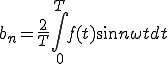
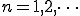 (1-4)
(1-4)
と比較すると同じになっていることが分かります。
これが射影の考え方です。
波の成分を各々のベクトルに投影する考えです。