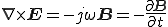 (1)
(1)
著者論文
いまマクスウェルの電磁界方程式を考える
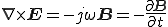 (1)
(1)
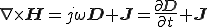 (2)
(2)
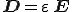 (3)
(3)
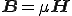 (4)
(4)
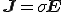 (5)
(5)
ここで、
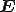 は電界[V/m],
は電界[V/m],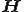 は磁界[A/m],
は磁界[A/m],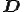 は電束密度
は電束密度 ![{\rm [C/m^2]} {\rm [C/m^2]}](BBFEB4D6CECEB0E8A4C8BCFEC7C8BFF4CECEB0E8_eq0009.gif) ,
,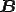 は磁束密度
は磁束密度 ![{\rm [Wb/m^2]} {\rm [Wb/m^2]}](BBFEB4D6CECEB0E8A4C8BCFEC7C8BFF4CECEB0E8_eq0011.gif) ,
,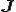 は電流密度
は電流密度 ![{\rm [A/m^2]} {\rm [A/m^2]}](BBFEB4D6CECEB0E8A4C8BCFEC7C8BFF4CECEB0E8_eq0013.gif)
である。
一般にすべての媒質は、誘電体と磁性体で構成されている。
そしてそれらは全て空間上はテンソルとして表すことができる。
![\[ \begin{array}{CC} B_{x} \\ B_{y} \\ B_{z} \end{array} \] = \[ \begin{array}{CC} \mu_{11}& \mu_{12}& \mu_{13}& \\ \mu_{21}& \mu_{22}& \mu_{23}& \\ \mu_{31}& \mu_{32}& \mu_{33}&\end{array} \] \[ \begin{array}{CC} H_x\\ H_y\\ H_z \end{array} \] \[ \begin{array}{CC} B_{x} \\ B_{y} \\ B_{z} \end{array} \] = \[ \begin{array}{CC} \mu_{11}& \mu_{12}& \mu_{13}& \\ \mu_{21}& \mu_{22}& \mu_{23}& \\ \mu_{31}& \mu_{32}& \mu_{33}&\end{array} \] \[ \begin{array}{CC} H_x\\ H_y\\ H_z \end{array} \]](BBFEB4D6CECEB0E8A4C8BCFEC7C8BFF4CECEB0E8_eq0014.gif)
テンソルは、媒質の空間においての性質を表します。
媒質の性質は、大きくわけて
の4種類に分けられる。
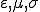 が、周波数により値が異なる場合、これを分散性媒質と呼ぶ。
が、周波数により値が異なる場合、これを分散性媒質と呼ぶ。
時間軸上での
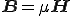
は、周波数軸上では、
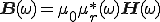 (2-1)
(2-1)
となる。つまり周波数の関数となっている。
磁性体の複素比透磁率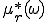 は,
は,
周波数無限大(時間領域でいえば瞬間の時間)のときの比透磁率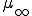 と電気比感受率(分極率)
と電気比感受率(分極率)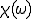 の和
の和
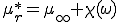 (2-2)
(2-2)
で表すことが出来る.
従って式(2-1)は,
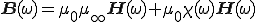 (2-3)
(2-3)
と表すことができる.
ここで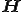 は磁界であり,
は磁界であり,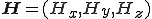 である.
である.
式(2-3)の第2項の周波数領域の掛け算は,時間領域では
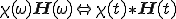 (2-4)
(2-4)
のように畳み込み定理により時間領域に変換できる。
式(2-4)は,
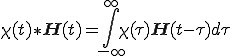 (2-5)
(2-5)
で表すことができる.
つまり周波数領域の掛け算は、時間領域での畳み込みとなり、畳みこみを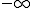 から
から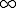 まで行ったものに等しいことがわかる。
まで行ったものに等しいことがわかる。
したがって時間領域での式(2-3)は,
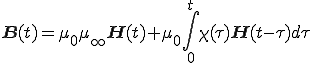 (2-6)
(2-6)
となる.