シミュレーティングで学ぶアナログ&ディジタルフィルタ入門 小野浩司著
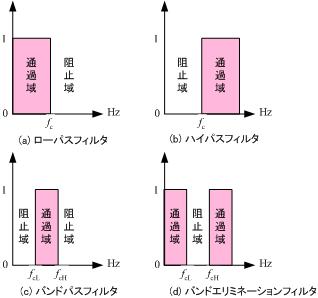
フィルタは必要な信号を取り出す。

フィルタに入力した信号の振幅が、何倍になって出力されるかを表現したもの。
通過域では1倍 -> 信号はそのまま通過する
阻止域では0倍 -> 信号は除去される
通過域と阻止域との境界にあたる周波数を、遮断周波数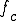 と呼ぶ。
と呼ぶ。
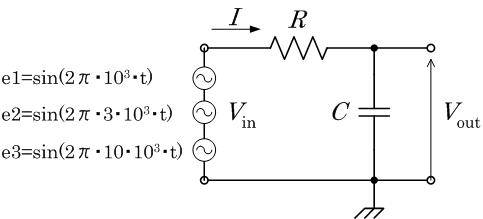
上記のようなCR回路を考える。
このCとRで構成される回路はローパスフィルタとなる。
このローパスフィルタの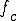 は、
は、
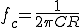
いま入力を
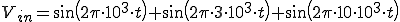
とする。つまり
1kHzの正弦波と3kHzの正弦波と10kHzの正弦波
をあわせたものである。
そして 100kHzと5kHzと0.5kHz以上を除去するローパスフィルタを作る。
| fc [kHz] | 100 | 5 | 0.5 |
| C [uF] | 0.01 | 0.01 | 0.1 |
| R [kΩ] | 0.159 | 3.18 | 3.18 |
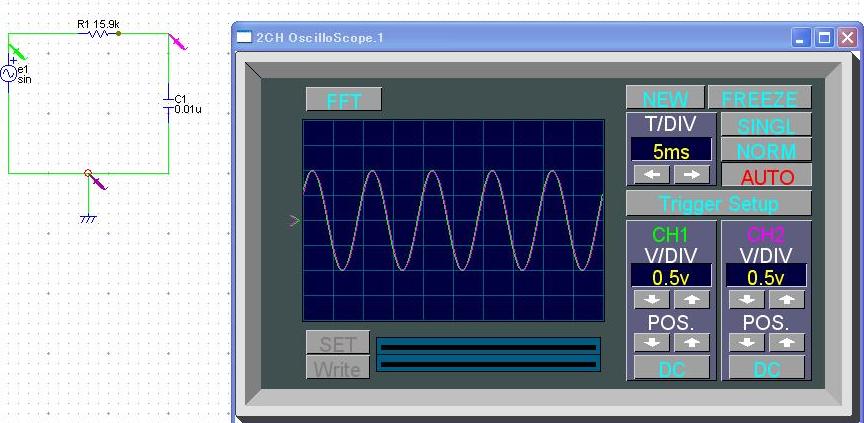
入力は緑、出力は赤
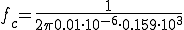
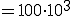
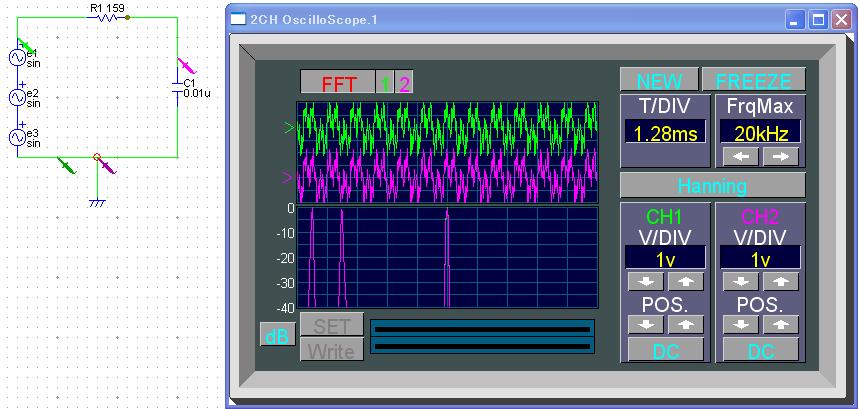
■結果
すべて通す
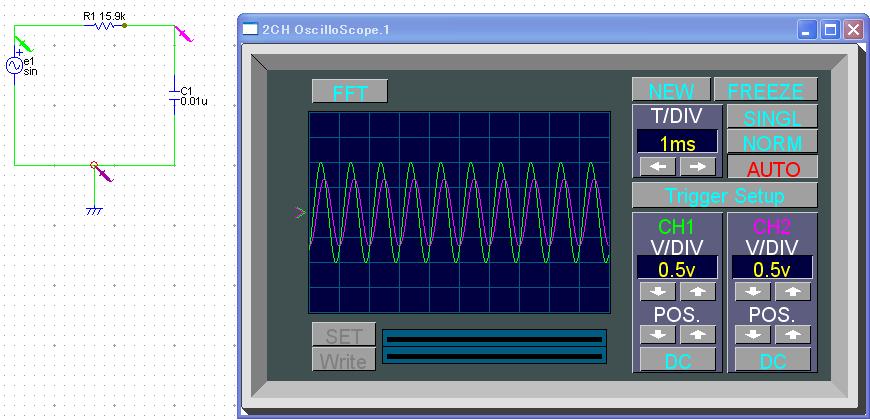
入力は緑、出力は赤
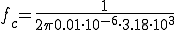
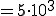
■結果
10kHz 減衰 5kHz すこし減衰 1kHz 通過
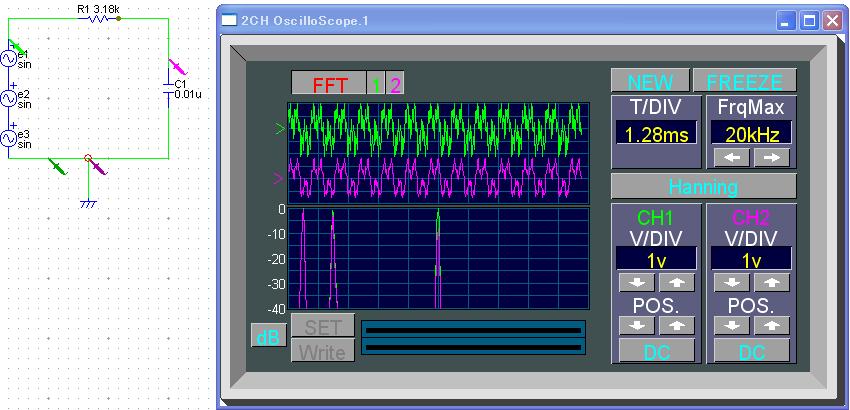
入力は緑、出力は赤
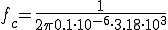
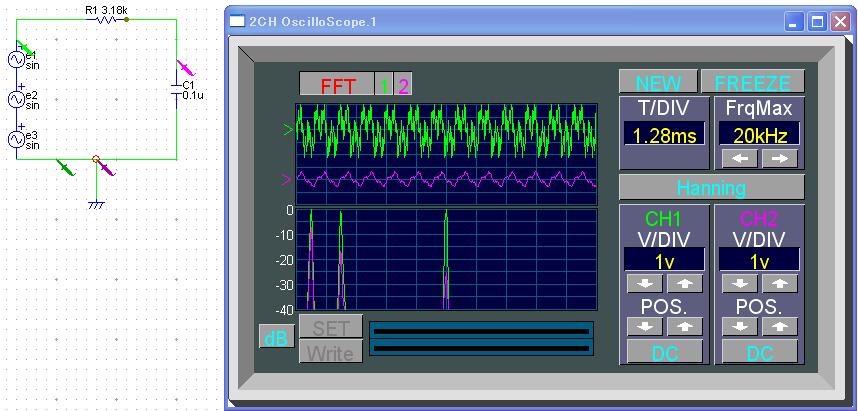
■結果
10kHz 減衰 5kHz 減衰 1kHz 減衰
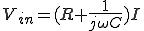
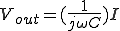
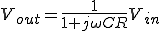
ここで、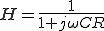
とすると
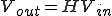

この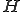 を伝達関数と呼ぶ。
を伝達関数と呼ぶ。
入力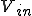 を
を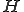 に印加したら出力
に印加したら出力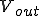 を得るという意味となる。
を得るという意味となる。
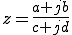 を極形式(オイラー版)を用いて表す。
を極形式(オイラー版)を用いて表す。
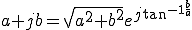
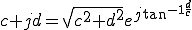
なので
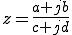
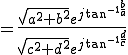
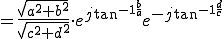

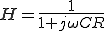 を極形式で表す
を極形式で表す
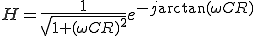
ここで、
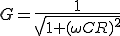
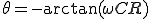
とすると

この は周波数領域の特性を示している。
は周波数領域の特性を示している。
ここで、
 :: 振幅特性 入力信号の振幅が何倍になるかを示す。
:: 振幅特性 入力信号の振幅が何倍になるかを示す。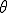 :: 位相特性 入力信号の位相がどれだけずれるかを示す。
:: 位相特性 入力信号の位相がどれだけずれるかを示す。
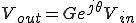
いま、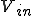 を正弦波とすれば
を正弦波とすれば
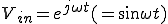 (1)
(1)
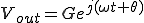
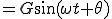 (2)
(2)
(1)と(2)を比較すると
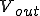 の振幅は、
の振幅は、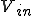 の
の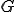 倍
倍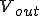 の位相は、
の位相は、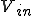 より
より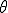 進んでいる
進んでいる
といえる。
振幅: 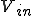 の
の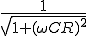
位相: 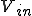 より
より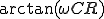 遅れる。
遅れる。
C=0.01[uF] , R=15.9[kΩ]のfc = 1kHzのローパスフィルタを考える。
1[rad]=180/pi=57.2958度
2pi[rad]で360度
CR = 0.01*10^-6*15.9*10^3 =1.5900e-004
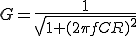
G=1/sqrt(1+(2*pi*0.1*10^3*CR)^2)=0.9950
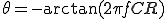
theta= -atan(2*pi*0.1*10^3*CR) = -0.0996[rad]
CR = 0.01*10^-6*15.9*10^3 =1.5900e-004
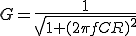
G=1/sqrt(1+(2*pi*1*10^3*CR)^2)=0.7075
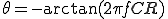
theta= -atan(2*pi*1*10^3*CR) = -0.7849[rad]
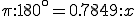
(180*0.7849)/pi = 44.9715度
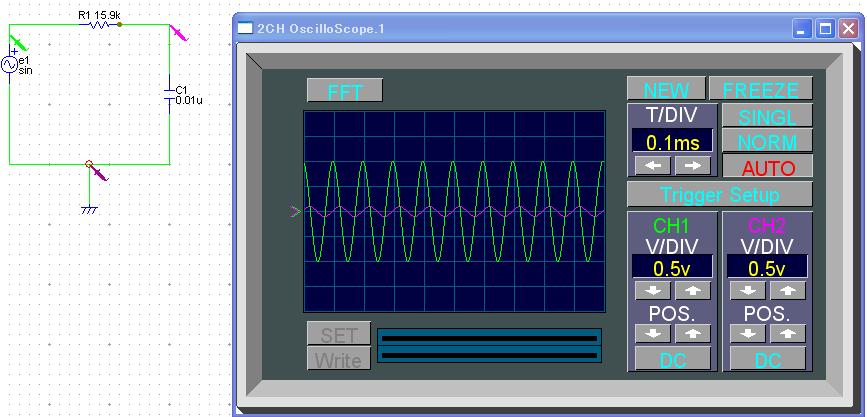
CR = 0.01*10^-6*15.9*10^3 =1.5900e-004
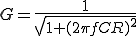
G=1/sqrt(1+(2*pi*10*10^3*CR)^2)= 0.0996
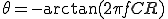
theta= -atan(2*pi*1*10^3*CR) = -1.4710[rad]
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% CR low-pass filter
% C=0.01[uF] , R=15.9[kΩ] fc = 1kHz
%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
echo off
clear all
close all
C=0.01e-6
R=15.9e3;
%%%%%%%% 振幅特性 %%%%%%%%%%%%%%%%
figure(1)
data=[];
freq=[];
for n=[0.01 0.05 0.07 0.1 0.3 0.5 0.7 1 3 5 7 10 30 50 70 100]
f=n*10^3;
freq=[freq,f];
G=1/sqrt(1+(2*pi*f*C*R)^2);
data=[data,G];
end
semilogx(freq,data,'r-','linewidth',3);
axis([0 Inf 0 Inf]);
grid on
xlabel('Frequency[Hz]','Fontsize',18)
ylabel('Gain','Fontsize',18)
h=legend('Amplitude Characteristic',...,
3);
set(h,'FontSize',18);
h=gca
set(h,'LineWidth',2,...,
'FontSize',18)
print -djpeg cr_fc_1khz_amp.jpg
%%%% 位相特性 %%%%%
figure(2)
data=[];
freq=[];
for n=[0.01 0.05 0.07 0.1 0.3 0.5 0.7 1 3 5 7 10 30 50 70 100]
f=n*10^3;
freq=[freq,f];
theta= -atan(2*pi*f*C*R);
data=[data,theta];
end
semilogx(freq,data,'b-','linewidth',3);
axis([0 Inf -Inf 0]);
grid on
xlabel('Frequency[Hz]','Fontsize',18)
ylabel('\theta [rad]','Fontsize',18)
h=legend('Phase Characteristic',...,
3);
set(h,'FontSize',18);
h=gca
set(h,'LineWidth',2,...,
'FontSize',18)
print -djpeg cr_fc_1khz_phase.jpg
%%%%%%%%%% End Of Macro %%%%%%%%%%%%%%%%
遮断周波数とは、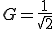 となる周波数
となる周波数
別の言い方をすると
遮断周波数とは、電力比が1/2となる周波数である。
電力は、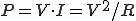
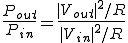
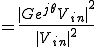
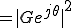
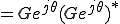
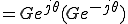
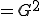
(ここで、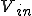 と
と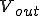 は複素数なので
は複素数なので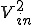 ではなく
ではなく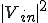 )
)
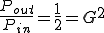
ゆえに
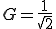
ここでCRローパスフィルタのGが1/2のときを求めると、
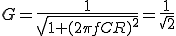
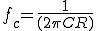
振幅特性 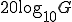 [dB]
[dB]
| 増幅率 G | 20log10G |
|---|---|
| 100000 | 100 |
| 10000 | 80 |
| 1000 | 60 |
| 100 | 40 |
| 10 | 20 |
| 1 | 0 |
| 1/√2=0.7 | -3 |
| 0.5 | -6 |
| 0.1 | -20 |
| 0.01 | -40 |
| 0.001 | -60 |
| 0.0001 | -80 |
| 0.00001 | -100 |
echo off
clear all
close all
C=0.01e-6
R=15.9e3;
%%%%%%%% 振幅特性 %%%%%%%%%%%%%%%%
figure(1)
data=[];
freq=[];
for n=[0.01 0.05 0.07 0.1 0.3 0.5 0.7 1 3 5 7 10 30 50 70 100]
f=n*10^3;
freq=[freq,f];
G=1/sqrt(1+(2*pi*f*C*R)^2);
G=20*log10(G);
data=[data,G];
end
semilogx(freq,data,'r-','linewidth',3);
axis([0 Inf -Inf Inf]);
grid on
xlabel('Frequency[Hz]','Fontsize',18)
ylabel('Gain[dB]','Fontsize',18)
h=legend('Amplitude Characteristic',...,
3);
set(h,'FontSize',18);
h=gca
set(h,'LineWidth',2,...,
'FontSize',18)
print -djpeg cr_fc_1khz_amp_db.jpg
%%%%%%%%%% End Of Macro %%%%%%%%%%%%%%%%
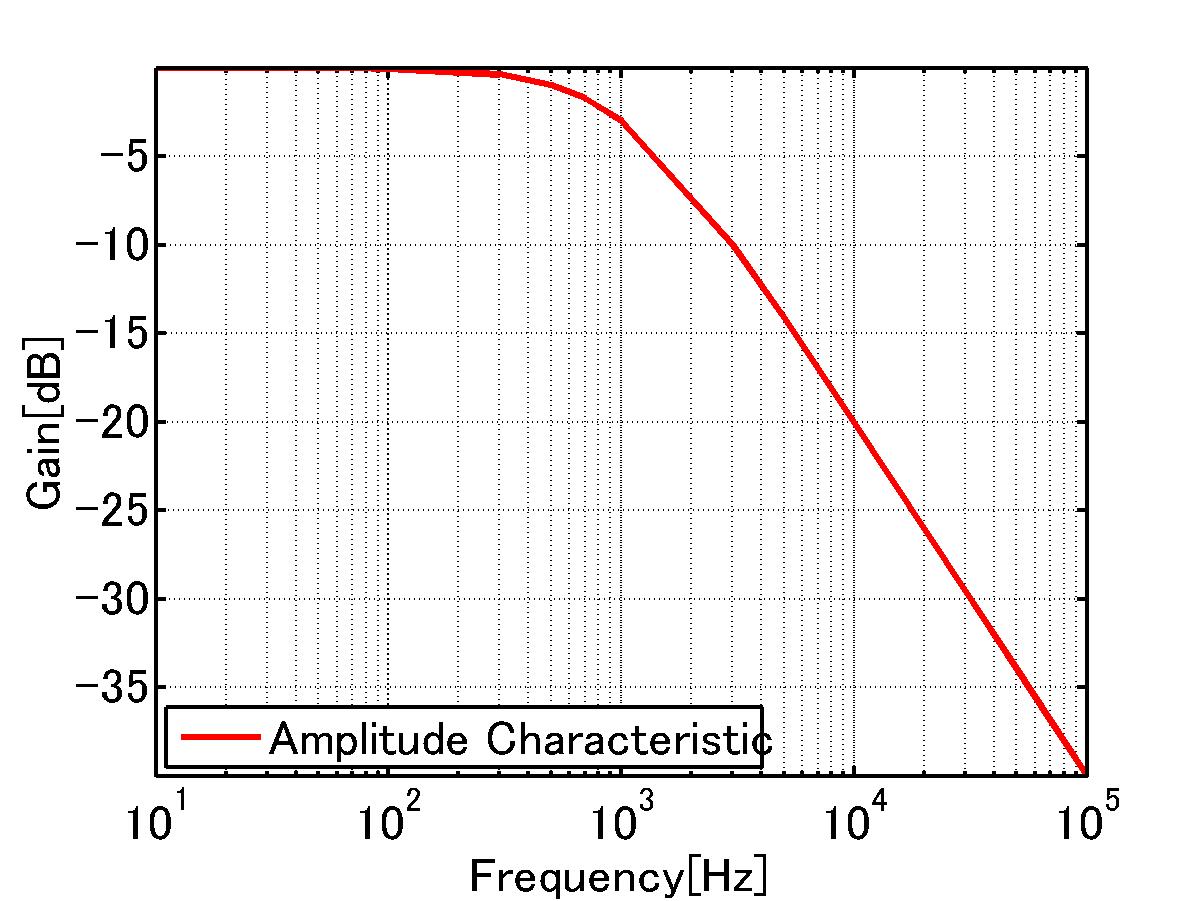

[dB/dec]について説明する。
decは、decade(ディケード、10で1つの塊の意)であり、
[dB/dec]とは、周波数が10倍になれば何[dB]下がるかを示している。
20[dB/dec]とは、周波数が10倍になると20dB下がることを示している。
[dB/oct]について説明する。
octは、octave(オクターブ、音階が1オクターブ上がると周波数は2倍)から来ている。
[dB/oct]とは、周波数が2倍になれば何[dB]下がるかを示している。
6[dB/oct]とは、周波数が2倍になると6dB下がることを示している。
[dB/dec]は、10倍の周波数をひとかたまりにしているため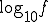
| f | ... | 0.1 | 1 | 10 | 100 | 1000 | ... |
|---|---|---|---|---|---|---|---|
| log10 f | ... | -1 | 0 | 1 | 2 | 3 | ... |
[dB/oct]は、2倍の周波数をひとかたまりにしているため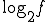
| f | ... | 0.5 | 1 | 2 | 4 | 8 | ... |
|---|---|---|---|---|---|---|---|
| log2 f | ... | -1 | 0 | 1 | 2 | 3 | ... |
つまり、
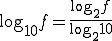
÷log2 10
--------->
[dB/dec] <--------- [dB/oct]
x log2 10
20 / log2(10) = 6 [dB/oct]
いま、振幅特性を理想的なものとし、位相特性だけを考える。

ローパスフィルタの遮断周波数をfc=3[Hz]
入力信号g(t)を1[Hz]と2[Hz]からなる
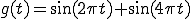
とする。
位相特性が異なる二つのフィルタに、入力信号g(t)を通したときの
出力波形を以下に示す。
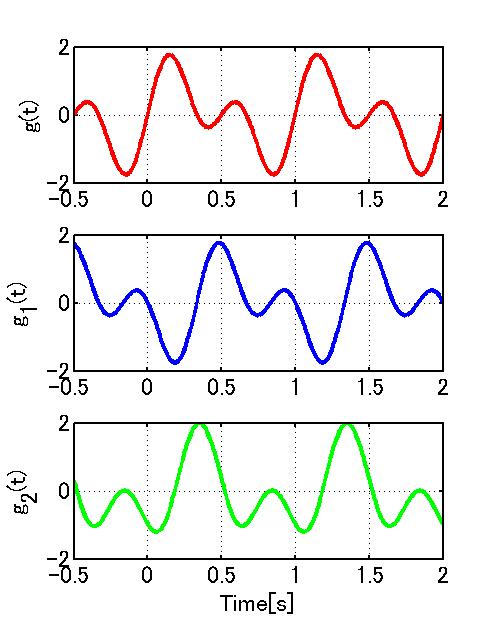
f_c = 3[Hz]であるため、(2-a),(2-b)とも信号は全て通過する。
(2-a)では、入力g(t)に比べ出力g1(t)は遅れて出力される。
位相特性が(2-a)のような直線位相特性の場合、出力は時間的に遅れる。
(2-b)では、入力g(t)に比べ出力g2(t)は波形の形も変形してしまっている。
位相特性が直線位相ではない場合、入力と出力のパターンは変化してしまう。
このように、
位相特性とは、出力信号のパターンが「変わってしまうのか」、「変わらないのか」を表している。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 位相特性のチェック
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
echo off
clear all
close all
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
subplot(3,1,1);
data=[];
time=[];
for t=[-0.5:0.01:2]
y=sin(2*pi*t)+sin(4*pi*t);
time=[time,t];
data=[data,y];
end
plot(time,data,'r-','linewidth',3);
axis([-0.5 2 -2 2]);
grid on
ylabel('g(t)','Fontsize',18)
h=gca
set(h,'LineWidth',2,...,
'FontSize',18)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% theta_1の出力
subplot(3,1,2);
data=[];
time=[];
for t=[-0.5:0.01:2]
y=sin(2*pi*t-2/3*pi)+sin(4*pi*t-4/3*pi);
time=[time,t];
data=[data,y];
end
plot(time,data,'b-','linewidth',3);
axis([-0.5 2 -2 2]);
grid on
ylabel('g_{1}(t)','Fontsize',18)
h=gca
set(h,'LineWidth',2,...,
'FontSize',18)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% theta_2の出力
subplot(3,1,3);
data=[];
time=[];
for t=[-0.5:0.01:2]
y=sin(2*pi*t-2/9*pi)+sin(4*pi*t-8/9*pi);
time=[time,t];
data=[data,y];
end
plot(time,data,'g-','linewidth',3);
axis([-0.5 2 -2 2]);
grid on
xlabel('Time[s]','Fontsize',18)
ylabel('g_{2}(t)','Fontsize',18)
h=gca
set(h,'LineWidth',2,...,
'FontSize',18)
print -djpeg isou_tokusei.jpg
%%%%%%%%%% End Of Macro %%%%%%%%%%%%%%%%
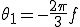
1[Hz]: 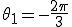
2[Hz]: 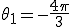
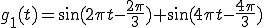
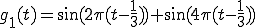
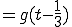
つまり、
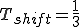 [s]
[s]
となり、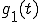 は、
は、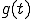 より1/3遅れて出力される。
より1/3遅れて出力される。
位相特性が直線位相
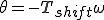
であれば、出力信号は入力信号に対して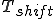 [s]ずれる。
[s]ずれる。
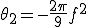
1[Hz]: 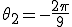
2[Hz]: 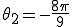
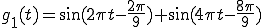
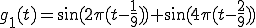
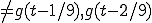
この式は、g(t)とg2(t)では波形それ自身のパターンが異なることを示している。
直線位相を有するフィルタは、フィルタリングされる信号のパターンそのものを重要視するときに使われる。
心電図などでは、波形そのものに重要な情報があるため、フィルタリングしたときに心電図が
歪んでしまっては正しく心電図を読むことができない。
このようなときは直線位相のフィルタが使われる。