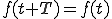
(1)「ディジタル信号処理技術」玉井徳みち、長島厚、藤田泰弘、若井修造著 日経BP社
(2)「ディジタル信号処理の基礎」三上直樹著 CQ出版
(3)「C言語によるディジタル信号処理入門」三上直樹著 CQ出版
(4)「アナログ&ディジタルフィルタ入門」小野浩司著 日刊工業
(5)「フーリエの冒険」ヒッポファミリークラブ
(6)「C言語で始める医用情報処理」小高知宏著 Ohmsha
(7)「量子力学の冒険」ヒッポファミリークラブ
(8)「最新ウェーブレット実践講座」戸田浩、章忠、川畑洋昭著 SoftBankCreative社
フーリエ級数展開の式はこうでした。
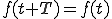
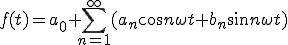 (1-1)
(1-1)
ここで、
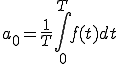 (1-2)
(1-2)
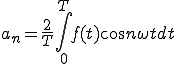
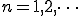 (1-3)
(1-3)
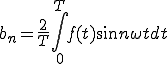
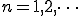 (1-4)
(1-4)
意味:周期のある複雑な波f(t)は単純な波の足し合わせで表すことができる
複素級数展開の式は、
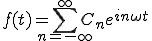 (2-11)
(2-11)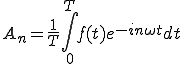
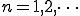 (2-6)
(2-6)
となります。これを以下で説明します。
ではまずオイラーの公式を思い出してください。
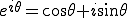
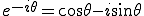
この式を変形すると
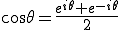 (2-1)
(2-1)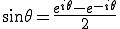 (2-2)
(2-2)
となります。
では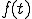 を変形してみましょう。
を変形してみましょう。
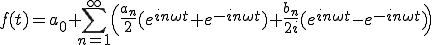
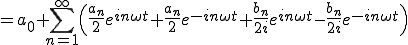
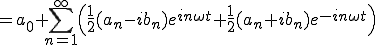 (2-3)
(2-3)
次にanを展開してみます。
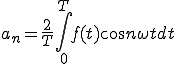
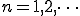 (1-3)
(1-3)
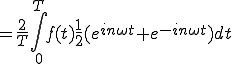
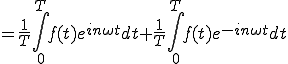 (2-4)
(2-4)
次にbnを展開
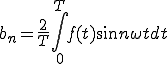
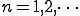 (1-3)
(1-3)
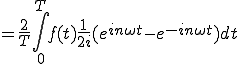
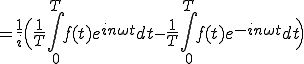
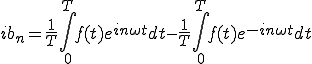 (2-5)
(2-5)
まとめてみます。
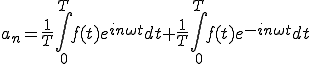 (2-4)
(2-4)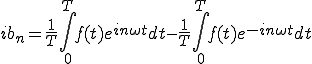 (2-5)
(2-5)
足し算 引き算をしあらたに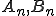 と名前をつけます。
と名前をつけます。
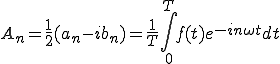 (2-6)
(2-6)
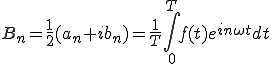 (2-7)
(2-7)
(2-3)に(2-6),(2-7)を代入すると
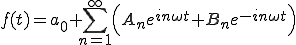 (2-8)
(2-8)
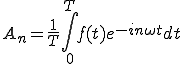 (2-6)
(2-6)
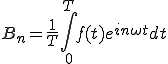 (2-7)
(2-7)
(2-8) 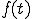 を分解します。
を分解します。
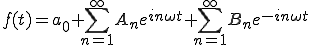 (2-9)
(2-9)
ここで第2項がn=0の時どうなるか見てましょう。
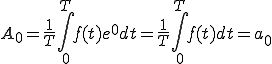
ということは?
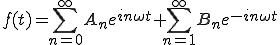 (2-10)
(2-10)
となります。次にBnを見ています。増分に-を付けてみると
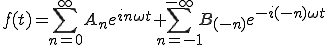
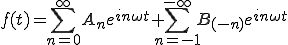
ところでBnは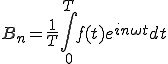 (2-7)
(2-7)
なので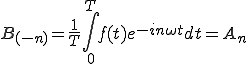
つまり、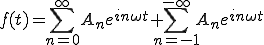
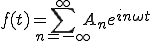 (2-8)
(2-8)
で波が表されることが分かります。
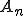 は,
は,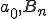 を含んでいるので、あらたに
を含んでいるので、あらたに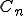 と名づけましょう。
と名づけましょう。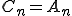 です。
です。
するとフーリエ級数展開式は
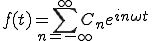 (2-11)
(2-11)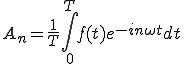 (2-6)
(2-6)
となります。