(1)「ディジタル信号処理技術」玉井徳みち、長島厚、藤田泰弘、若井修造著 日経BP社
(2)「ディジタル信号処理の基礎」三上直樹著 CQ出版
(3)「C言語によるディジタル信号処理入門」三上直樹著 CQ出版
(4)「アナログ&ディジタルフィルタ入門」小野浩司著 日刊工業
(5)「フーリエの冒険」ヒッポファミリークラブ
(6)「C言語で始める医用情報処理」小高知宏著 Ohmsha
(7)「量子力学の冒険」ヒッポファミリークラブ
(8)「最新ウェーブレット実践講座」戸田浩、章忠、川畑洋昭著 SoftBankCreative社
フーリエ級数展開の式はこうでした。
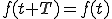
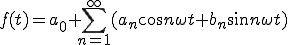 (1-1)
(1-1)
ここで、
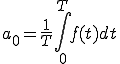 (1-2)
(1-2)
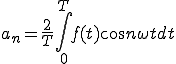
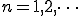 (1-3)
(1-3)
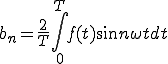
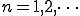 (1-4)
(1-4)
複素級数展開の式は、
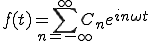 (1-5)
(1-5)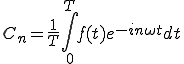
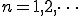 (1-6)
(1-6)
とでした。
意味:周期のある複雑な波f(t)は単純な波の足し合わせで表すことができる
なのですが,いろいろと疑問はあります。
疑問その1 周期がある波なら良いのですが周期のない波はどうやったら表せるのか?
疑問その2 周期のある波も長い間観察すれば周期がないかも知れない。
そこで周期が無限大の波を観察することにすれば、
周期がある波もない波も同じように
無限の周期がある波としてみることができるはずです。
ところで波は基本周波数の整数倍として表すことができました。
基本周波数は
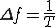
基本周波数= 1/周期
で表すことができます。
その基本周波数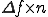 倍の各々の波が表せたわけです。
倍の各々の波が表せたわけです。
ところで今回は周期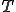 を無間大にするのですから
を無間大にするのですから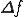 は0に非常に近くなるはずです。
は0に非常に近くなるはずです。
周期が決まっている場合は周波数は離散的(飛び飛びの値を取る)であったが
周期を無限大に取ると周波数(スペクトル)は連続になる。
つまり
周期が分からない(周期を無限と仮定した場合の)周波数領域への変換をフーリエ変換と言うのです。
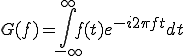 (2-2)
(2-2)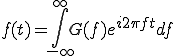 (2-3)
(2-3)
を以下で求めてみる。
基本周波数を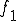 , 2番目の周波数を
, 2番目の周波数を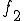 n番目を
n番目を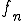 とすると
とすると
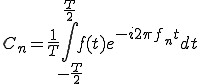
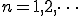 (1-6)
(1-6)
となります。
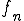 は離散的な値(とびとびの値)です。(ようするに
は離散的な値(とびとびの値)です。(ようするに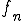 と
と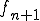 との間に空きがある)。
との間に空きがある)。
ここで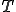 を連続にすると周波数は連続になるので
を連続にすると周波数は連続になるので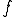 と表して良いこととなる。
と表して良いこととなる。
ここで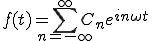 (1-5)
(1-5)
は
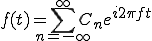
となるからここに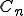 を代入すると
を代入すると
 (2-1)
(2-1)
ここで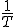 は
は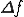 だったから
だったから
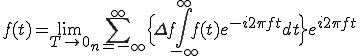 (2-1b)
(2-1b)
となる。
ここで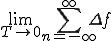
の部分は積分となるので
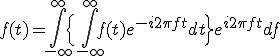 (2-1c)
(2-1c)
となります。
今カッコの中は、時間の積分となっていて、未知数は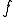 ですから
ですから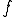 つまり周波数の関数と見なせます。
つまり周波数の関数と見なせます。
そこで、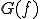 とすると
とすると
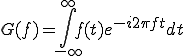 (2-2)
(2-2)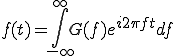 (2-3)
(2-3)
となり、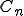 に相当するところが
に相当するところが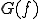 となったわけです。
となったわけです。
これで周期が分からなくても周波数成分を求めることができます(連続なスペクトルとして)。
これをフーリエ変換と言います。
そしてスペクトルからf(t)を求めることはフーリエ逆変換と言います。
今、時間軸上でずーと1であるスペクトルを求めてみる。
ためしに周期が-ΔT/2〜ΔT/2であるものとして計算する。
それ以外の領域は見えていないものとして0とする。
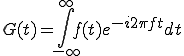 (2-2)
(2-2)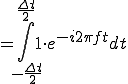
![= \Big[ \frac{-1}{i2\pi f} e^{-i 2\pi f t} \Big]^{\frac{\Delta t}{2}}_{-\frac{\Delta t}{2}} = \Big[ \frac{-1}{i2\pi f} e^{-i 2\pi f t} \Big]^{\frac{\Delta t}{2}}_{-\frac{\Delta t}{2}}](A5D5A1BCA5EAA5A8CAD1B4B940B4F0CBDC_eq0045.gif)
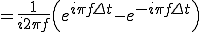
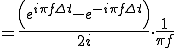
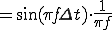
となります。ここで公式
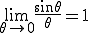
という公式を使います。
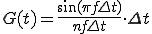
つまりfが0に近づくときG(f)はΔtとなるわけです。Δtというのは観測する間隔でした観測する間隔を変えていったらスペクトルはどうなるかを見てみます。
図を見ると分かりますように周期Δtを長くすればするほどスペクトルは真値に近づきます。
つまりフーリエ変換の式は
「どんな複雑な波でも(たとえ周期がなくとも)単純な波一つ一つに分解できる」
だけでなく
「見る時間によってそれがどの位の確からしさでいえるかという不確定さまでも含む式」
なのでした。