(1)「ディジタル信号処理技術」玉井徳みち、長島厚、藤田泰弘、若井修造著 日経BP社
(2)「ディジタル信号処理の基礎」三上直樹著 CQ出版
(3)「C言語によるディジタル信号処理入門」三上直樹著 CQ出版
(4)「アナログ&ディジタルフィルタ入門」小野浩司著 日刊工業
(5)「フーリエの冒険」ヒッポファミリークラブ
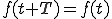
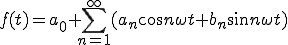
ここで、
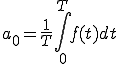
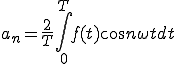
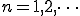
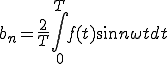
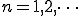
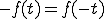 奇関数
奇関数
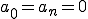
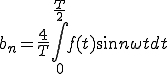
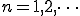
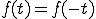 偶関数
偶関数
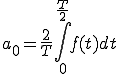
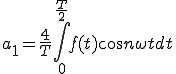
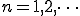
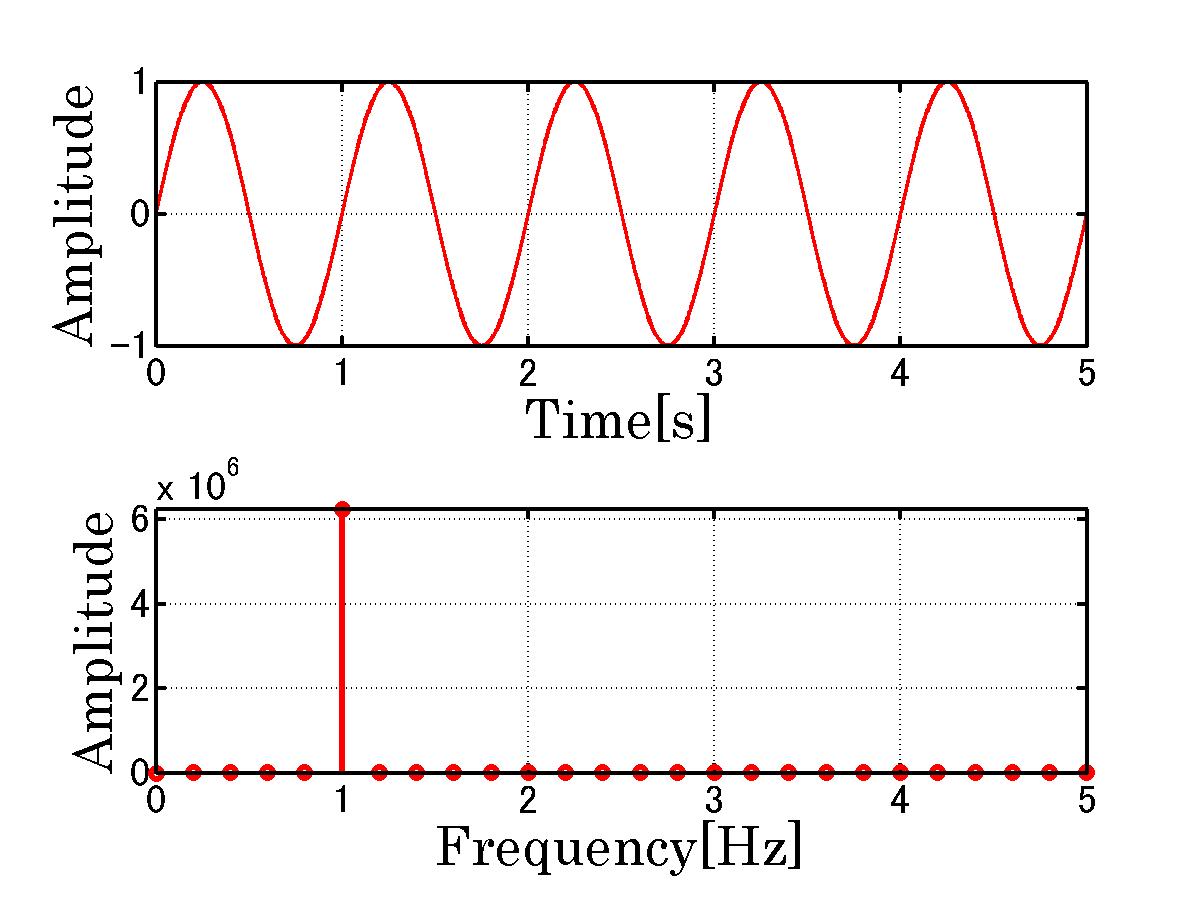
1Hzの正弦波を5周期分 サンプリング周期 1 [ms] サンプリング周波数 1 [kHz] データ総数 5001 基本周波数 0.2[Hz]
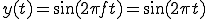
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 正弦波形を表示
% programming by embedded.samurai
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
echo off
clear all
close all
%サンプリング周期 1[ms]
dx=1e-3;
%サンプリング周波数 1kHz
dfs=1/dx
% xの範囲は 0から0.001単位で5まで
x=[0:dx:5];
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
subplot(2,1,1);
f=1; %1[Hz]
y1=sin(2*pi*f*x);
xx = x/pi;
plot(x,y1,'r-','linewidth',2);
% 文字の大きさ、線の太さの設定
set(gca,'LineWidth',2,...,
'FontSize',15);
xlabel('Time[s]','Fontsize',20,'FontName','Century');
ylabel('Amplitude','Fontsize',20,'FontName','Century');
% x-y範囲
axis([-Inf Inf -Inf Inf]);
grid on
hold on;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
subplot(2,1,2);
%データ総数
[gyo N]=size(x)
%基本周波数
df=dfs/N
%FFTの結果は複素数である
fftdata1 = fft(y1)';
%FFTの絶対値を求める
power1=abs(fftdata1).^2;
%離散周波数を作る
freq = [0:N-1]'*df;
stem(freq,power1,'r-','linewidth',3);
hold on
grid on
axis([0 5 0 Inf]);
set(gca,'LineWidth',2,...,
'FontSize',15);
xlabel('Frequency[Hz]','Fontsize',20,'FontName','Century');
ylabel('Amplitude','Fontsize',20,'FontName','Century');
print -djpeg sinwave_f.jpg
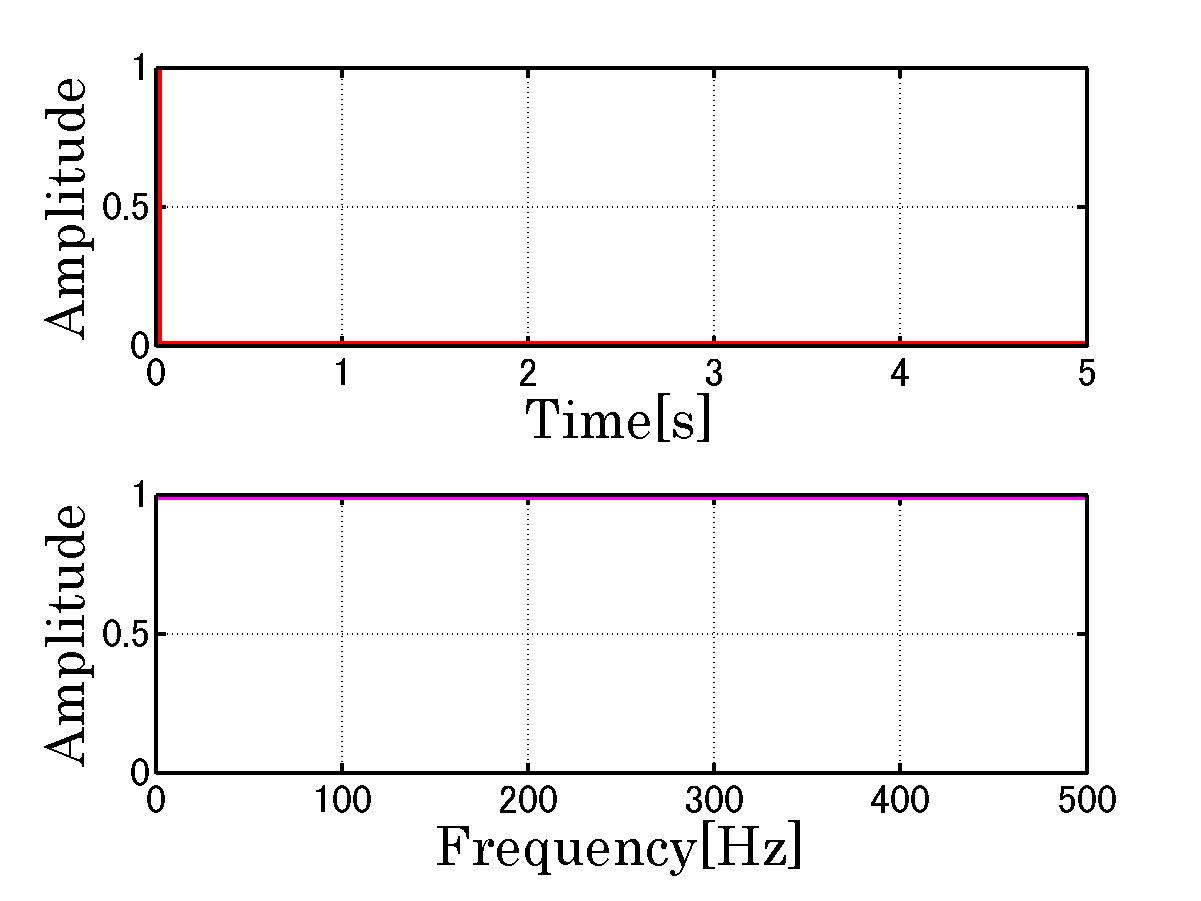
サンプリング周期 1 [ms] サンプリング周波数 1 [kHz] データ総数 5001 基本周波数 0.2[Hz]
インパルス信号とは、
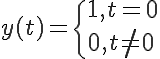
のように表される信号である。
インパルス信号を周波数に変換すると図のようにすべての周波数帯において
周波数が広がっていることが分かる。
インパルス信号はものすごく大事である。
なぜなら全ての周波数を含む信号だからである。
全ての周波数を信号が含むことができれば、ある媒質の周波数応答
つまり何Hzの信号は反射し、何Hzの信号は透過するかといったことを
調べることができるようになる。
例えば,
入射波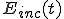 をインパルス信号とし、
をインパルス信号とし、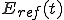 を反射した信号としたとき、
を反射した信号としたとき、
それらをフーリエ変換し,
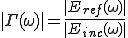
とすると周波数全域に対しての反射係数を求めることができる。
しかしながら理想的なインパルス信号を実世界で作ることは不可能なので
実際には、周波数を広く含む信号を用いて反射係数を求めるのにはガウスパルスなどが使われる。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% インパルス波形を表示
% programming by embedded.samurai
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
echo off
clear all
close all
%サンプリング周期 1[ms]
dx=1e-3;
dfs=1/dx
% xの範囲は 0から0.001単位で5まで
x=[0:dx:5];
%データ総数
[gyo N]=size(x)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
subplot(2,1,1);
% インパルス信号を作る
y1=[1;zeros(N-1,1)];
plot(x,y1,'r-','linewidth',5);
% 文字の大きさ、線の太さの設定
set(gca,'LineWidth',2,...,
'FontSize',15);
xlabel('Time[s]','Fontsize',20,'FontName','Century');
ylabel('Amplitude','Fontsize',20,'FontName','Century');
% x-y範囲
axis([-Inf Inf -Inf Inf]);
grid on
hold on;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
subplot(2,1,2);
%サンプリング周波数 1kHz
dfs=1/dx;
%データ総数
[gyo N]=size(x)
%基本周波数
df=dfs/N
%FFTの結果は複素数である
fftdata1 = fft(y1)';
%FFTの絶対値を求める
power1=abs(fftdata1).^2;
%離散周波数を作る
freq = [0:N-1]'*df;
plot(freq,power1,'m-','linewidth',5);
hold on
grid on
axis([0 dfs/2 0 Inf]);
set(gca,'LineWidth',2,...,
'FontSize',15);
xlabel('Frequency[Hz]','Fontsize',20,'FontName','Century');
ylabel('Amplitude','Fontsize',20,'FontName','Century');
print -djpeg impulsu_wave_f.jpg
//******************************************************
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 三角波形を表示
% programming by embedded.samurai
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
echo off
clear all
close all
%サンプリング周期 1[ms]
dx=1e-3;
% xの範囲は -pi/2から0.001単位で3piまで
x=[0:dx:3*pi];
xx = x/pi;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% n=1のとき
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
figure(1);
y1=0;
for m=1:1:1
y=(4/m)*(-1)^(m+1)*sin(m.*x);
y1=y1+y;
end
plot(xx,y1/pi,'r-','linewidth',3);
hold on;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% n=10のとき
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
y2=0;
for m=1:1:10
y=(4/m)*(-1)^(m+1)*sin(m.*x);
y2=y2+y;
end
plot(xx,y2/pi,'g-','linewidth',3);
hold on;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% n=100のとき
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
y3=0;
for m=1:1:100
y=(4/m)*(-1)^(m+1)*sin(m.*x);
y3=y3+y;
end
plot(xx,y3/pi,'m-','linewidth',3);
hold on;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 理想パルス
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
data=[];
for n=x
if (n < pi)
y=2*n;
data=[data,y];
elseif (n >= pi) && (n <= 3*pi)
y=2*n -4*pi;
data=[data,y];
end
end
plot(xx,data/pi,'b-','linewidth',3);
hold on;
% xラベルとその文字の大きさ、線の太さの設定
str1={'-3p','-2p','-p','0','p','2p','3p'}
set(gca,'FontName','symbol','xtick',[-3:1:3],'xticklabel',str1)
str2={'-3p','-2p','-p','0','p','2p','3p'}
set(gca,'FontName','symbol','ytick',[-3:1:3],'yticklabel',str2)
set(gca,'LineWidth',2,'FontSize',18)
% x-y範囲
axis([-Inf Inf -Inf Inf]);
grid on
% xラベル、yラベル
xlabel('Positon t','Fontsize',20,'FontName','Century');
ylabel('pulsu wave y(t)','Fontsize',20,'FontName','Century')
% キャプション
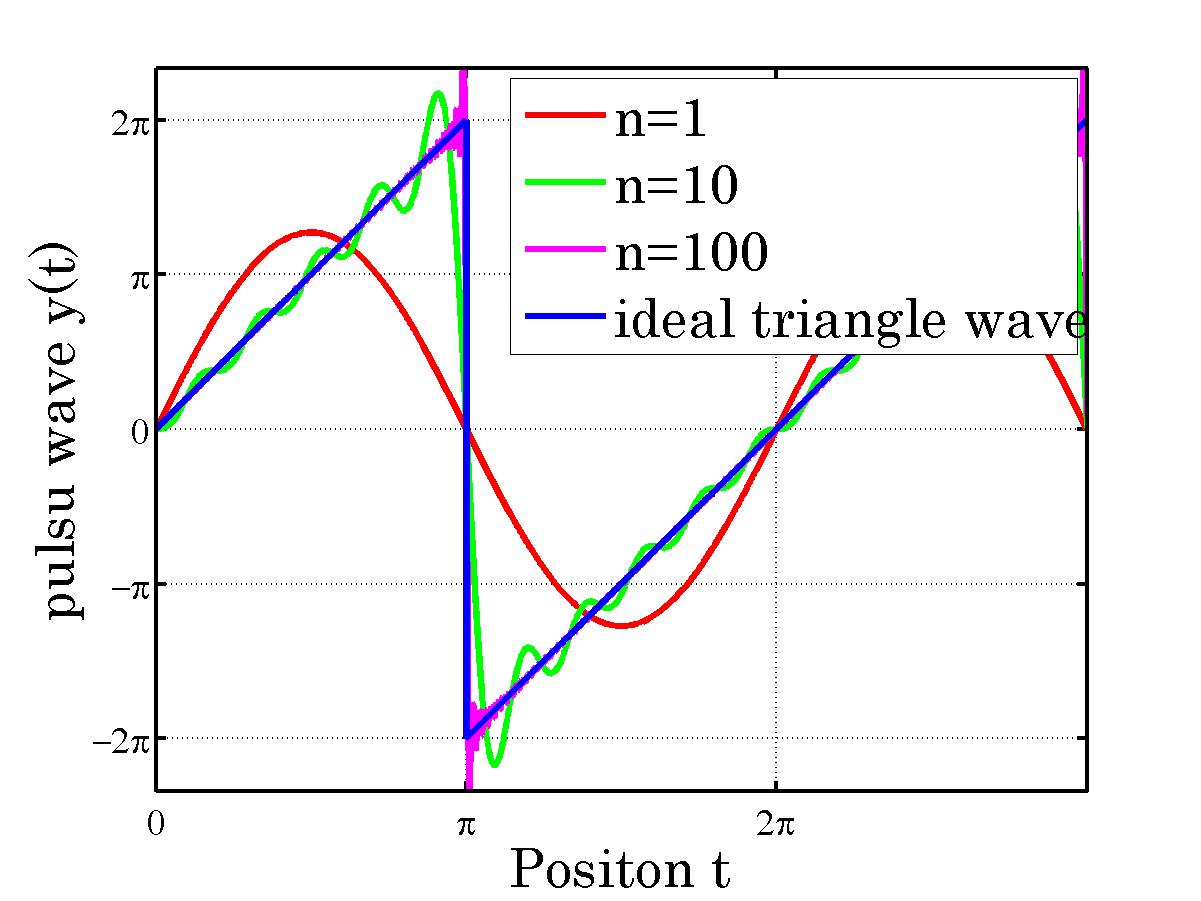
h=legend('n=1',...,
'n=10',...,
'n=100',...,
'ideal triangle wave',...,
1);
set(h,'FontSize',20,'FontName','Century');
print -djpeg sankakuwave_t.jpg
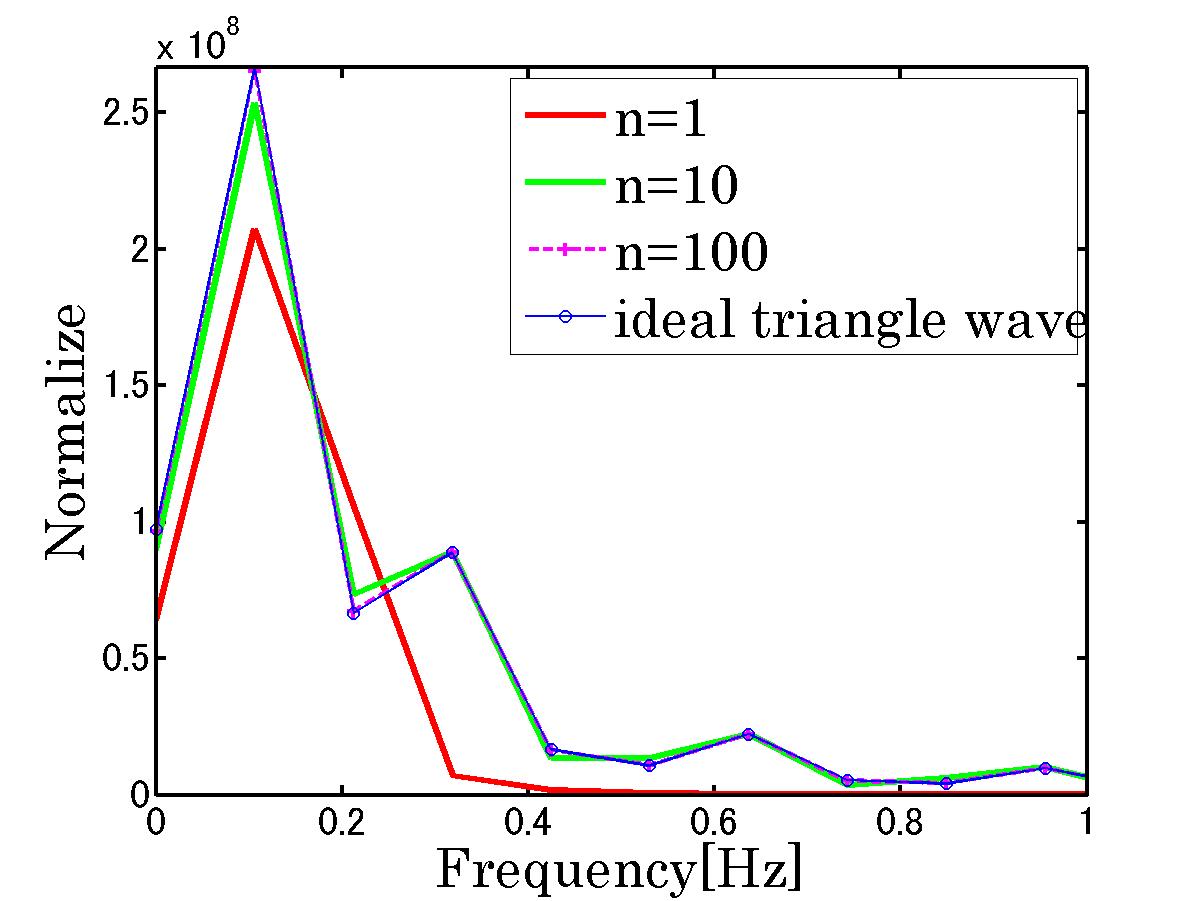
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
figure(2);
%サンプリング周波数 1kHz
df=1/dx
%xの数 7854
[gyo retu]=size(x)
%基本周波数 0.1273[Hz]
bf=df/retu
%FFTの結果は複素数である
fftdata1 = fft(y1)';
fftdata2 = fft(y2)';
fftdata3 = fft(y3)';
fftdata4 = fft(data)';
%FFTの絶対値を求める
power1=abs(fftdata1).^2;
power2=abs(fftdata2).^2;
power3=abs(fftdata3).^2;
power4=abs(fftdata4).^2;
%離散周波数を作る
freq = [0:retu-1]'*bf
plot(freq,power1,'r-','linewidth',3);
hold on
plot(freq,power2,'g-','linewidth',3);
hold on
plot(freq,power3,'m+--','linewidth',2);
hold on
plot(freq,power4,'bo-','linewidth',1);
hold on
axis([0 1 0 Inf]);
set(gca,'LineWidth',2,...,
'FontSize',15);
xlabel('Frequency[Hz]','Fontsize',20,'FontName','Century');
ylabel('Normalize','Fontsize',20,'FontName','Century');
% キャプション
h=legend('n=1',...,
'n=10',...,
'n=100',...,
'ideal triangle wave',...,
1);
set(h,'FontSize',20,'FontName','Century');
print -djpeg sankakuwave_f.jpg
■問い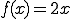 を
を 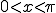 なる区間でフーリエ展開する。
なる区間でフーリエ展開する。
■解答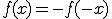 奇関数
奇関数
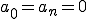
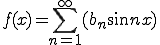
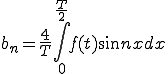
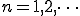
ここで 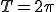 なので
なので
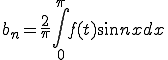
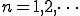
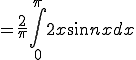
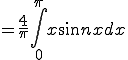
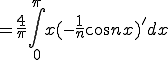
![= \frac{4}{\pi}\{ \[-\frac{x}{n} \cos nx\]^{\pi}_{0} + \int_0^{\pi}(\frac{1}{n} \cos n x) dx \} = \frac{4}{\pi}\{ \[-\frac{x}{n} \cos nx\]^{\pi}_{0} + \int_0^{\pi}(\frac{1}{n} \cos n x) dx \}](C6FECECFBFAEB9E6_eq0034.gif)
![= \frac{4}{\pi}\{ -\frac{\pi}{n} \cos n \pi + \frac{1}{n}\[\frac{1}{n} \sin n x \]^{\pi}_{0} \} = \frac{4}{\pi}\{ -\frac{\pi}{n} \cos n \pi + \frac{1}{n}\[\frac{1}{n} \sin n x \]^{\pi}_{0} \}](C6FECECFBFAEB9E6_eq0035.gif)
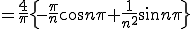
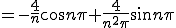
![= \frac{4}{n} \[ \frac{ \sin n \p}{n \pi} - \cos n \pi \] = \frac{4}{n} \[ \frac{ \sin n \p}{n \pi} - \cos n \pi \]](C6FECECFBFAEB9E6_eq0038.gif)
ここで第1項は0しかとらない。第2項は、-1,1,-1,1..となるが先頭に-があるため 1,-1,1,-1
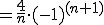
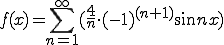
これはMalabソース
y=(4/m)*(-1)^(m+1)*sin(m.*x);
と同じになる。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% パルス波形を表示
% programming by embedded samurai
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
echo off
clear all
close all
%サンプリング周期 1[ms]
dx=1e-3;
% xの範囲は -pi/2から0.001単位で2piまで
x=[-pi/2:dx:2*pi];
xx = x/pi;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 注意!
% cos(n*x) n=omega
% n=omega=1,2,..,n である。
% omega = 2*pi*f = 1,2,...,n の意味なので
% 周波数的には、
% f= 1/2pi,2/2pi,3/2pi,...,n
% = 0.1592[Hz],0.3183[Hz],0.4775[Hz],0.6366[Hz],
% = 0.7958[Hz],0.9549[Hz],1.1141[Hz],....,n
%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 1[Hz]を表示
% ここはテスト
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
figure(1);
ty1=sin(2*pi*1*x);
%1[Hz]に近い
ty2=sin(6.2832*x);
plot(xx,ty1,'r-','linewidth',2);
hold on;
plot(xx,ty2,'b--','linewidth',3);
% xラベルとその文字の大きさ、線の太さの設定
str={'-p/2','0','p/2','p','3p/2','2p'}
set(gca,'FontName','symbol','xtick',[-0.5:.5:2],'xticklabel',str)
set(gca,'LineWidth',2,'FontSize',18)
% x-y範囲
axis([-Inf Inf -Inf Inf]);
grid on
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% n=1のとき
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
figure(2);
y1=0;
for m=0:1:0
y=(4/pi)*(1/(2*m+1))*(-1)^m*cos((2*m+1).*x);
y1=y1+y;
end
plot(xx,y1,'r-','linewidth',3);
hold on;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% n=10のとき
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
y2=0;
for m=0:1:10
y=(4/pi)*(1/(2*m+1))*(-1)^m*cos((2*m+1).*x);
y2=y2+y;
end
plot(xx,y2,'g-','linewidth',3);
hold on;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% n=100のとき
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
y3=0;
for m=0:1:100
y=(4/pi)*(1/(2*m+1))*(-1)^m*cos((2*m+1).*x);
y3=y3+y;
end
plot(xx,y3,'m-','linewidth',3);
hold on;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 理想パルス
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
data=[];
for n=x
if (n < pi/2)
y=1;
data=[data,y];
elseif (n >= pi/2) && (n <= 3*pi/2)
y=-1;
data=[data,y];
elseif ( n > 3*pi/2)
y=1;
data=[data,y];
end
end
plot(xx,data,'b-','linewidth',3);
hold on;
% xラベルとその文字の大きさ、線の太さの設定
str={'-p/2','0','p/2','p','3p/2','2p'}
set(gca,'FontName','symbol','xtick',[-0.5:.5:2],'xticklabel',str)
set(gca,'LineWidth',2,'FontSize',18)
% x-y範囲
axis([-Inf Inf -Inf Inf]);
grid on
% xラベル、yラベル
xlabel('Positon t','Fontsize',20,'FontName','Century');
ylabel('pulsu wave y(t)','Fontsize',20,'FontName','Century')
% キャプション
h=legend('n=1',...,
'n=10',...,
'n=100',...,
'ideal pulsu',...,
1);
set(h,'FontSize',20,'FontName','Century');
print -djpeg pulsuwave_t.jpeg
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
figure(3);
%サンプリング周波数 1kHz
df=1/dx
%xの数 7854
[gyo retu]=size(x)
%基本周波数 0.1273[Hz]
bf=df/retu
%FFTの結果は複素数である
fftdata1 = fft(y1)';
fftdata2 = fft(y2)';
fftdata3 = fft(y3)';
fftdata4 = fft(data)';
%FFTの絶対値を求める
power1=abs(fftdata1).^2;
power2=abs(fftdata2).^2;
power3=abs(fftdata3).^2;
power4=abs(fftdata4).^2;
%離散周波数を作る
freq = [0:retu-1]'*bf
plot(freq,power1,'r-','linewidth',3);
hold on
plot(freq,power2,'g-','linewidth',3);
hold on
plot(freq,power3,'m+--','linewidth',2);
hold on
plot(freq,power4,'bo-','linewidth',1);
hold on
axis([0 1 0 Inf]);
set(gca,'LineWidth',2,...,
'FontSize',15);
xlabel('Frequency[Hz]','Fontsize',20,'FontName','Century');
ylabel('Normalize','Fontsize',20,'FontName','Century');
% キャプション
h=legend('n=1',...,
'n=10',...,
'n=100',...,
'ideal pulsu',...,
1);
set(h,'FontSize',20,'FontName','Century');
print -djpeg pulsuwave_f.jpg
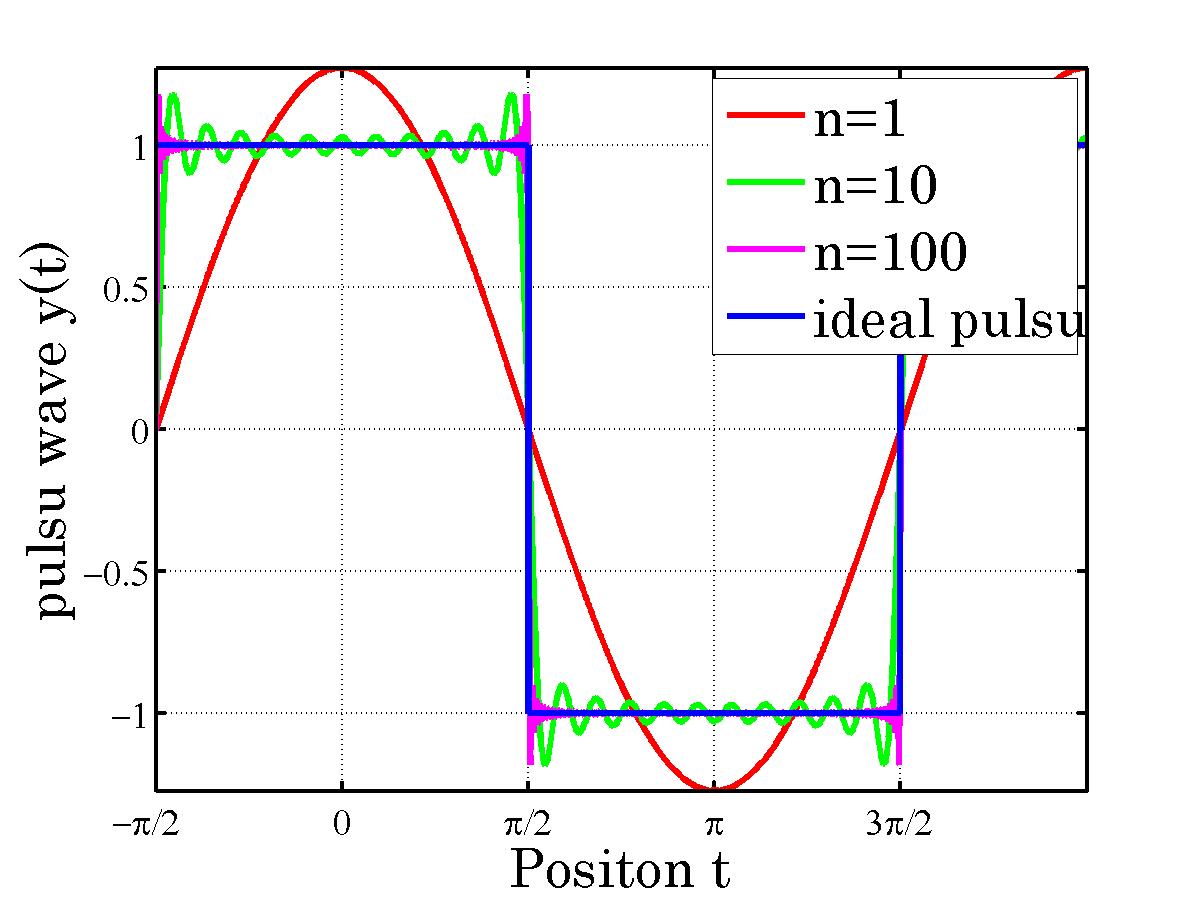
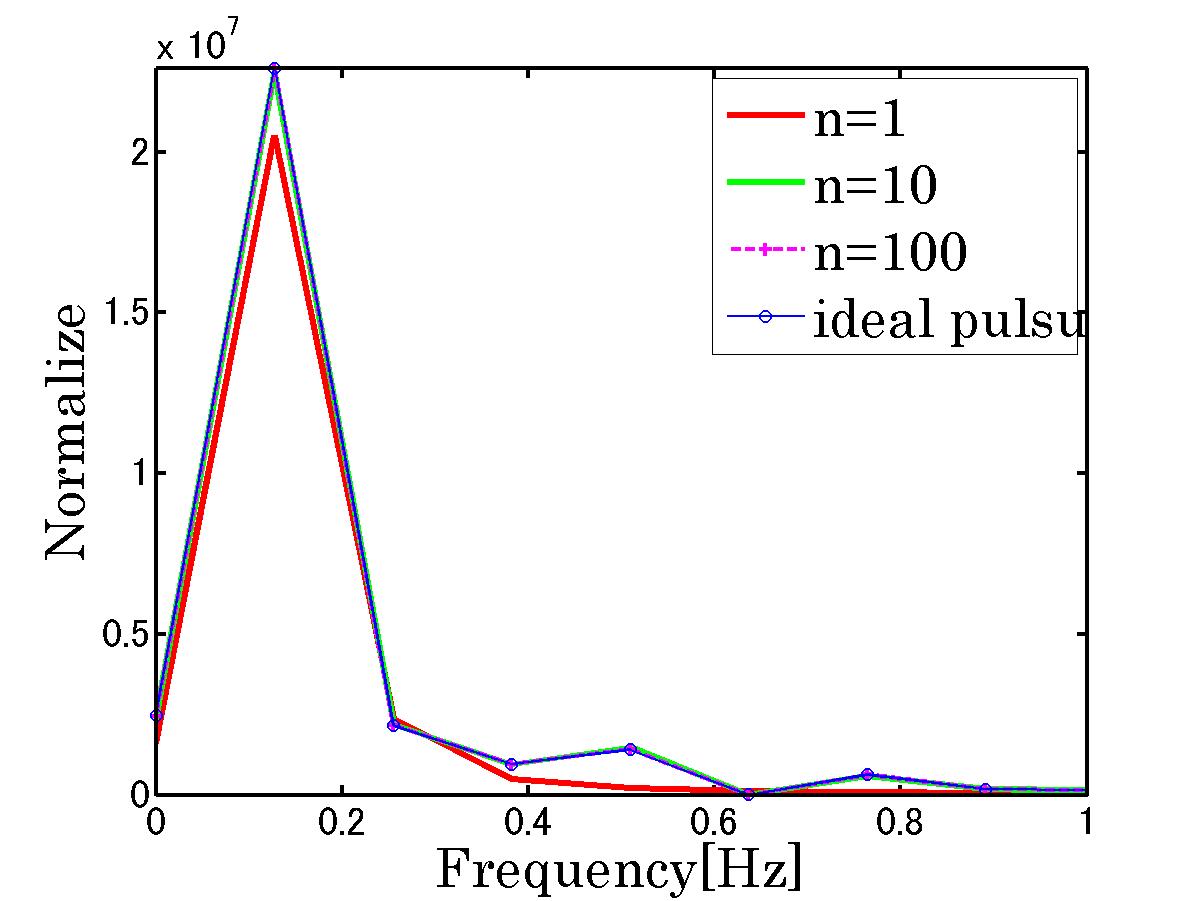
■問い
上図をフーリエ展開する
■解答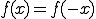 偶関数 サインの項 0
偶関数 サインの項 0
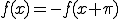
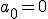
 は奇数項のみ
は奇数項のみ
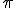 だけずれたときは
だけずれたときは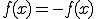 の奇関数となるから、
の奇関数となるから、
偶数のときは奇関数となる。コサインの項が消える。
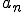 は奇数項のみ
は奇数項のみ 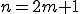 (m=0,1,2,3)
(m=0,1,2,3)
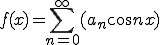
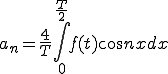
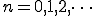
ここで 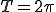 かつ
かつ 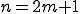
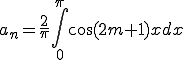
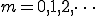
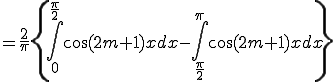
![= \frac{2}{\pi}\{ \[\frac{ \sin(2m+1)x}{(2m+1)} \]^{\frac{\pi}{2}}_{0} - \[\frac{ \sin(2m+1)x}{(2m+1)} \]^{\pi}_{\frac{\pi}{2}} \} = \frac{2}{\pi}\{ \[\frac{ \sin(2m+1)x}{(2m+1)} \]^{\frac{\pi}{2}}_{0} - \[\frac{ \sin(2m+1)x}{(2m+1)} \]^{\pi}_{\frac{\pi}{2}} \}](C6FECECFBFAEB9E6_eq0057.gif)
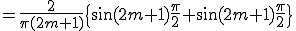
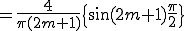
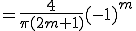
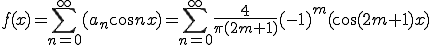
これはMalabソース
y=(4/pi)*(1/(2*m+1))*(-1)^m*cos((2*m+1).*x);
と同じになる。