(1)「ディジタル信号処理技術」玉井徳みち、長島厚、藤田泰弘、若井修造著 日経BP社
(2)「ディジタル信号処理の基礎」三上直樹著 CQ出版
(3)「C言語によるディジタル信号処理入門」三上直樹著 CQ出版
(4)「アナログ&ディジタルフィルタ入門」小野浩司著 日刊工業
(5)「フーリエの冒険」ヒッポファミリークラブ
(6)「C言語で始める医用情報処理」小高知宏著 Ohmsha
(7)「量子力学の冒険」ヒッポファミリークラブ
(8)「最新ウェーブレット実践講座」戸田浩、章忠、川畑洋昭著 SoftBankCreative社
(9)「ウェーブレットによる信号処理と画像処理」中野宏毅、山本鎭男、吉田靖夫著 共立出版
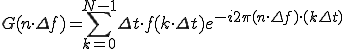
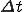 : 値を読んだ間隔(サンプリング周期)
: 値を読んだ間隔(サンプリング周期)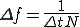 : 基本周波数
: 基本周波数
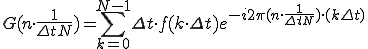
いま、簡単化のために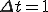 とすると
とすると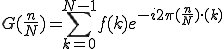
Nは定数となりますので、
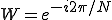
と表します。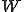 を回転子と言います。
を回転子と言います。
すると式は
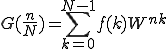
となります。ではN=8のときを計算してみましょう。
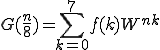
これを n=0〜7まで計算しましょう。
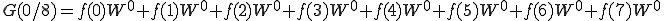
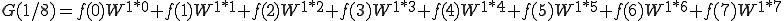
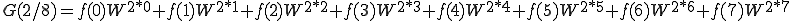
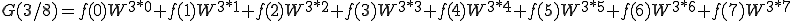
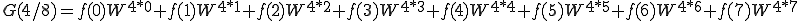
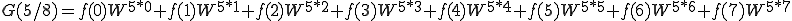
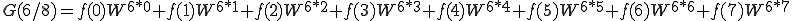
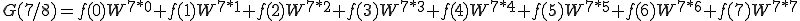
これは、
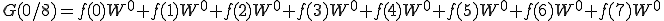
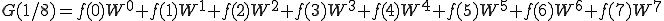
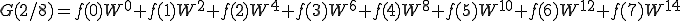
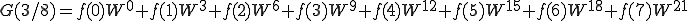
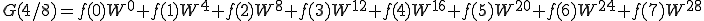
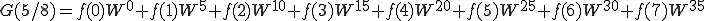
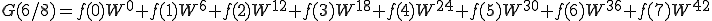
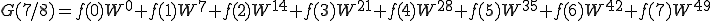
こうなります。
64回の積和演算をしなくはいけません。これを減らすことができるのでしょうか?
表にしてみましょう。

図1-1
先ほどWは回転子と言うと言いました。
ではなぜ回転子と言うのでしょうか?
ここでWは何だったのかを思い出してみましょう。
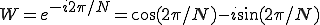
は円周状の点yを正弦波,xを余弦波で表されるものだから結局周期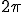
でぐるぐる回っている現象を表している。
そして今は、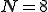 なのでこの回転は図のように8分割されて回転していることになるのです。
なのでこの回転は図のように8分割されて回転していることになるのです。
ということは
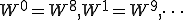 と書きかえられるので、
と書きかえられるので、
図1-2
となります。
図1-3
すると偶数組みの方は上半分と下半分が同じです。
これを使えば計算量を半分にできそうです。
でも奇数組がいまいちです。
ひとまず、偶数組と奇数組に分けてみましょう。
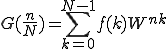
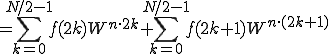
ここで、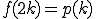
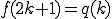
として書き直します。
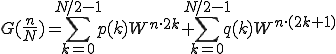
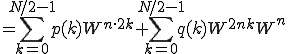
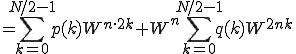
ここで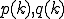 は、
は、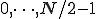 までで
までで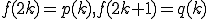 ですから
ですから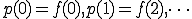 という関係を忘れないようにすること。
という関係を忘れないようにすること。
ところで奇数項は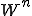 が飛び出たので
が飛び出たので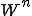 を引いてもう一度図を書き直しましょう。
を引いてもう一度図を書き直しましょう。

図1-4
これで
奇数 偶数とも上半分だけで計算することができるようになりました。
計算回数は
偶数16回+奇数16回 + W^nをかける回数4回=36回
で計算することができるようになりました。
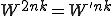 とおく
とおく
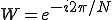
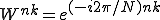
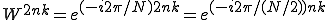
となって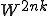 になると円は4等分になります。そこで
になると円は4等分になります。そこで
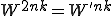
とすることで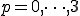 までの式で表すことができます。つまり
までの式で表すことができます。つまり
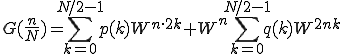
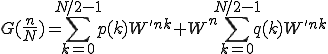
と表すことができます。
ではそれに習い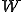 を
を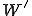 にしてしまいましょう。
にしてしまいましょう。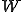 の肩を2で割れば良いのです。
の肩を2で割れば良いのです。
図1-5
今度はそう上半分と下半分が同じなので
上半分だけ考えてこれをまた2等分できるかどうかやってみる。
図1-6
式は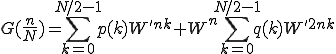
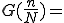
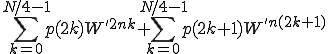
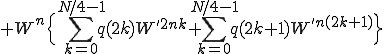
ここで
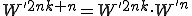
なので先ほどと同じように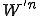 を前に出す。
を前に出す。
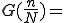
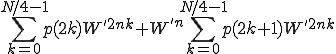
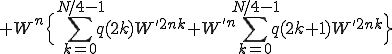
となる。
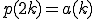
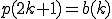
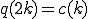
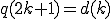 とおく
とおく
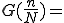
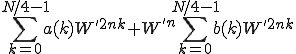
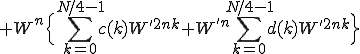
また同じように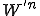 でくくって引くと
でくくって引くと
図1-7
図のようになります。
ここで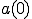 とか
とか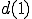 はなんだったのでしょう。
はなんだったのでしょう。
思い出してみます。
図1-8
ここで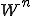 は8等分のWだから45度位相がずれる波となる。
は8等分のWだから45度位相がずれる波となる。
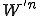 は4等分のWだから90度位相がずれる波となります。
は4等分のWだから90度位相がずれる波となります。
だから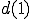 なんかは、まず45度ずれてさらに90度ずれる波を求めていることになります。
なんかは、まず45度ずれてさらに90度ずれる波を求めていることになります。
結局
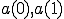 : 4回
: 4回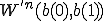 4回+2回
4回+2回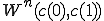 4回+2回
4回+2回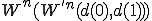 4回+2回+2回
4回+2回+2回計24回の計算時間の短縮になるというわけです。
演算の流れをもう一度よく見てシグナルフローグラフを作ってみましょう。
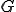 を
を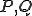 で表す
で表す

図1-5
図は,2個の4点DFTになっていました。
偶数の4点DFTを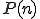 ,奇数の4点DFTを
,奇数の4点DFTを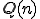 として表しましょう。
として表しましょう。
ためしに最初の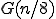 の偶数部分を
の偶数部分を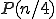 で表すと
で表すと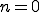 の場合は、
の場合は、
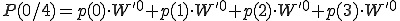
となります。
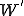 は4等分された回転子ですので
は4等分された回転子ですので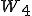 としましょう。
としましょう。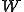 は
は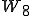 としましょう。
としましょう。
書き直すと
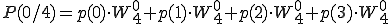
です。全部表して見ましょう。
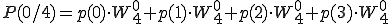
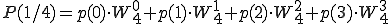
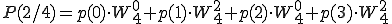
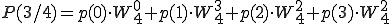
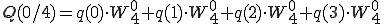
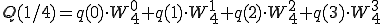
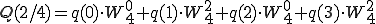
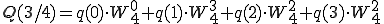
奇数はpがqになっただけです。
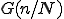 は
は
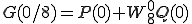
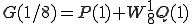
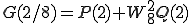
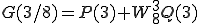
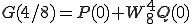
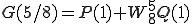
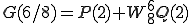
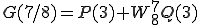
は、180度回転することは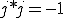 をかけることになるから
をかけることになるから
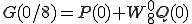
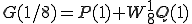
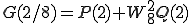
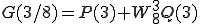
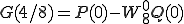
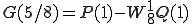
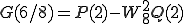
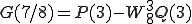
と実際は計算されます。ここで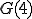 以降の第2項に-が付いているのは
以降の第2項に-が付いているのは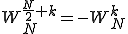
という規則があるからです。
回転子が90度回転するのと虚数jを掛けるのは同じです。
つまり半周期(180度)回転したものはjxj=-1を掛けたものに等しいという条件です。
これらすべてを加味してグラフにすると以下のようになります。
ピンクはWが掛かった線,青線は-の線です。
これを見ると4回の掛け算+8回の加算で計算することができます。
このようなグラフをシグナルフローグラフ、
FFTのこのような演算をバタフライ演算といいます。
この図はP,Qが求まったとして話が始まっています。
今度はP,Qについて同じことをしなければなりません。
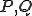 を
を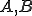 で表す
で表す

図1-7
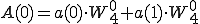
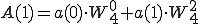
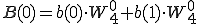
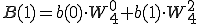
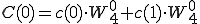
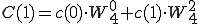
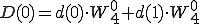
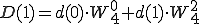
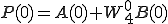
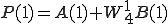
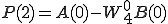
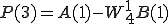
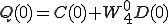
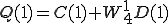
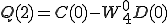
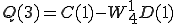
4点DFT(P,Q)も2点DFT で表すことができました。
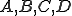 を
を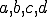 で表す
で表す
最後に1点DFTの形を作ってa(0),a(1),b(0),b(1),c(0),c(1),d(0),d(1)までで表します。
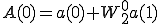
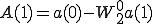
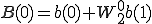
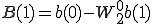
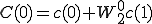
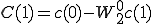
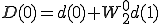
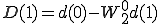
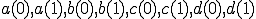 を
を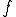 に戻す
に戻すで戻す。
これをプログラミングすることで周波数領域を求めることができます。
このf(0),f(4),f(2),f(6),f(1),f(5),f(3),f(7)という並びですがこれどうやってこの順番割り出すのでしょう。
これはビットで見ると分かります。
最初私達は2つのグループを偶数と奇数に分けました。
そこで
(1) 偶数を0 奇数を1として並べてみます。
0 0 0 0 1 1 1 1
次にそのそれぞれのグループをまた2つに並べました。そこで
(2) また0,1で並べます。
0 0 0 0 1 0 1 0 0 1 0 1 1 1 1 1
(3) 最後にまたまた分割したものを並べます。
0 0 0 ->0 1 0 0 ->4 0 1 0 ->2 1 1 0 ->6 0 0 1 ->1 1 0 1 ->5 0 1 1 ->3 1 1 1 ->7
0 0 0->0 0 0 1->1 0 1 0->2 0 1 1->3 1 0 0->4 1 0 1->5 1 1 0->6 1 1 1->7
逆に表示してみると今度はきれいな数字の列になりました。
コンピュータで計算するときは
与えられたデータの最上位Bit(MSB)と最下位Bit(LSB)を交換すればよい
そして得られた番号に格納されたデータと最初のデータを交換すればよい
これはFFTをやる前とした後のどちらにも適用できますが本図ではFFTをする前の場合です。
このFFTをCooley Tukeyの時間間引きFFTと言います。
#include "common.h"
/***********************************************************************
* NAME : fft_table
* FUNCTION: FFTで使用するテーブルを作成する
* PROCESS : 省略
*
* INPUT : @param double wn_FFT[] -回転因子Wnのための配列
* : @param short br_FFT[] -ビット逆順のための配列
* : @param int N_FFT -FFTする全データ数
*
* OUTPUT : @param double wn_FFT[] -生成された回転因子Wnのための配列
* : @param short br_FFT[] -生成されたビット逆順のための配列
*
* RETURN : none
* CALL : none
/**********************************************************************/
void fft_table(double wn_FFT[],short br_FFT[],int N_FFT)
{
int i,n_half,ne,jp;
double arg;
int fft34=0;
//calculation of twiddle factor
arg = 2*PI / N_FFT;
fft34 = (N_FFT*3)/4;
for(i=0;i<fft34;i++){
wn_FFT[i] = (double)cos(arg*i);
#if DEBUG
printf("cos=%lf\tsin=%lf\n",cos(arg*i),sin(arg*i));
#endif
}
//calculation of bit reversal table
n_half = N_FFT/2;
br_FFT[0] = 0;
#if DEBUG
printf("br_FFT[%d]=0x%x\n",0,br_FFT[0]);
#endif
for(ne=1;ne<N_FFT;ne=ne<<1){
#if DEBUG
printf("ne=%d\n",ne);
#endif
for(jp=0;jp<ne;jp++){
br_FFT[jp+ne] = br_FFT[jp] + n_half;
#if DEBUG
printf("br_FFT[%d]=0x%x\n",jp+ne,br_FFT[jp+ne]);
#endif
}
n_half = n_half >> 1;
}
}//end of fft_table
/***************************************************************
* NAME : swap
* FUNCTION: データをひっくり返す
* PROCESS : 省略
* INPUT : @param double *a -データ
* : @param double *b -データ
*
* RETURN : none
* CALL : none
**************************************************************/
void swap(double *a,double *b){
double tmp;
tmp = *a;
*a = *b;
*b = tmp;
}
/***************************************************************
* NAME : fft5
* FUNCTION: 時間間引きFFT
* PROCESS : 直接sin cosを計算する 三上直樹氏のプログラムを改良
*
* INPUT : @param double real[] - FFTしたいデータ
* : @param double imag[] - FFTしたいデータ(全データ0を入れる)
* : @param short bitreverse[] - ビット逆順配列
* : @param int fftNum - FFTしたい全データ数(2の倍数)
*
* OUTPUT : @param double real[] - FFTされたデータ
* : @param double imag[] - FFTされたデータ
*
* RETURN : none
* CALL : none
**************************************************************/
void time_fft(double real[],double imag[],short bitreverse[],int fftNum)
{
double xtmpr,xtmpi;
int j,jnh,k,jxC,jxS,n_half,n_half2;
int step;
double arg;
for(j=0;j<fftNum;j++){
//条件判定ない場合 ひっくり返したあとまたひっくり返すので注意!!
if(j<bitreverse[j]){
swap(&real[j],&real[bitreverse[j]]);
swap(&imag[j],&imag[bitreverse[j]]);
}
}
n_half = 1;
n_half2 = 2;
for(step=fftNum/2;step >= 1 ;step = step/2){
for(k=0;k<fftNum;k=k+n_half2){
#if DEBUG
printf("k=%d\n",k);
#endif
jxC = 0;
jxS = fftNum / 4;
for(j=k;j< (k+n_half);j++){
#if DEBUG
printf("j=%d\t",j);
#endif
//jに対してn_half分移動したところと両者を演算する
jnh = j + n_half;
xtmpr = real[jnh];
xtmpi = imag[jnh];
arg = 2*PI / fftNum;
real[jnh] = xtmpr*cos(arg*jxC) + xtmpi * sin(arg*jxC);
imag[jnh] = xtmpi*cos(arg*jxC) - xtmpr * sin(arg*jxC);
#if DEBUG
printf("arg*jxC=%lf\n",arg*jxC);
#endif
xtmpr = real[j];
xtmpi = imag[j];
real[j] = xtmpr + real[jnh];
imag[j] = xtmpi + imag[jnh];
real[jnh] = xtmpr - real[jnh];
imag[jnh] = xtmpi - imag[jnh];
//回転子は次の演算領域に入ると1/2倍ずつ増える
jxC = jxC + step;
//jxS = jxS + step;
}
}
n_half = n_half * 2;
n_half2 = n_half2 * 2;
}
}
サンプリング時間を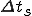
サンプリング周波数を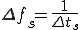
データ総数を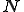
基本周波数 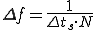
時間信号を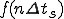 とすると
とすると
それを離散フーリエ変換したものは、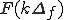 となる。
となる。
したがって、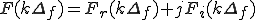
振幅スペクトル: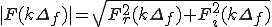
位相スペクトル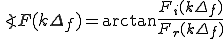
Matlabでは
fft
という命令だけでFFTしてくれるが使い方に注意!
以下にサンプルで示す。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Matlab FFT sample program
% programming by embedded.samurai
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
echo off
clear all
close all
%サンプリング周期 50[ms]
dt=50e-3;
%サンプリング周波数20Hz 10Hz以下まで表すことができる
df=1/dt;
%離散時間(横軸)を作る
t=[0:dt:50];
%50msごとの離散時間が何個で構成されるか調べる
[gyo retu]=size(t)
%gyo行、retu列の0データを作る。
zerodata = zeros(gyo,retu);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 1Hz+2Hz+5Hzの正弦波を表示する
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
subplot(2,1,1);
f1=1; %1[Hz]
f2=2; %2[Hz]
f3=5; %5[Hz]
if 1
y1=sin(2*pi*f1*t);
else
y1=zerodata; %0でもうまくいく
end
if 1
y2=sin(2*pi*f2*t);
else
y2=0;
end
if 1
y3=sin(2*pi*f3*t);
else
y3=0;
end
y=y1+y2+y3;
% 1+2+5Hzの正弦波を表示する
plot(t,y,'ro-','linewidth',2);
%stem(t,y,'ro-');
hold on;
axis([0 5 -Inf Inf]);
h=gca;
set(h,'LineWidth',2,...,
'FontSize',15);
xlabel('Time[s]','Fontsize',15);
ylabel('Amplitude','Fontsize',15)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 周波数スペクトルを表示する
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
subplot(2,1,2);
data=[];
%基本周波数の導出 基本周波数=サンプリング周波数/データ数
basicfre = df/retu
%FFTの結果は複素数である。複素数はテキストデータで保存できない
fftdata = fft(y(1:retu))';
%分解して、テキストとして保存する
fftdata_re = real(fftdata);
fftdata_im = imag(fftdata);
%離散周波数を作る
data = [data,[0:retu-1]'*df/retu];
%FFTの実部を格納する
data = [data,fftdata_re];
%FFTの虚部を格納する
data = [data,fftdata_im];
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 周波数スペクトルの絶対値を求める
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%FFTの絶対値を求める
power=abs(fftdata).^2;
maxpower = max(power);
%Normalize(正規化する)
Nmpower = power/maxpower;
%Normalize + [dB/dec]
NmpowerDB = 20*log10(power/maxpower);
%正規化データを格納する
data = [data,Nmpower];
%正規化データ[dB/dec]を格納する
data = [data,NmpowerDB];
plot(data(:,1),data(:,4),'b-','linewidth',2);
axis([0 df/2 0 1]);
h=gca;
set(h,'LineWidth',2,...,
'FontSize',15);
xlabel('Frequency[Hz]','Fontsize',15);
ylabel('Normalize','Fontsize',15);
save fftdata.txt data -ascii
print -djpeg fft_sample.jpg
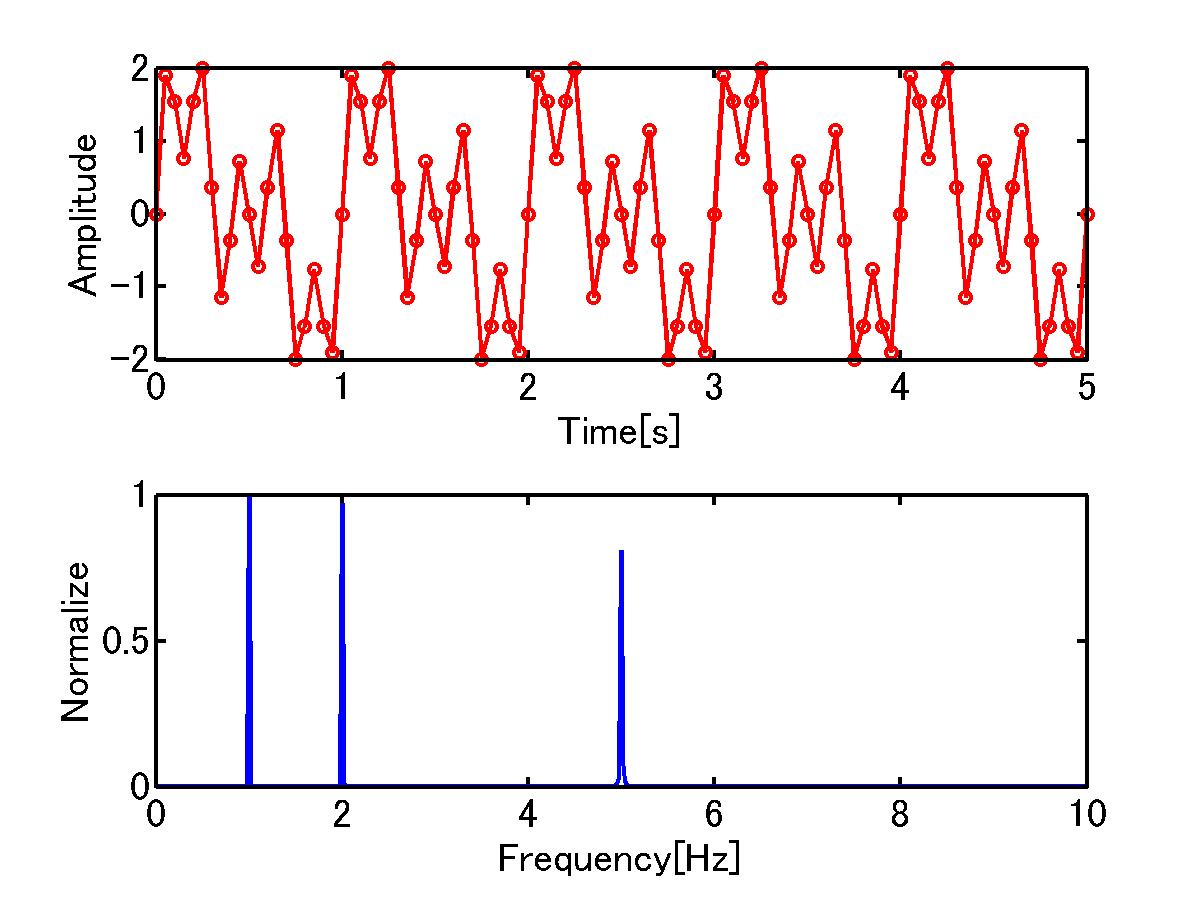
周波数 FFTの実部 FFTの虚部 FFTの絶対値 FFTの絶対値[dB/dec] 0.0000000e+000 -8.5997875e-013 -0.0000000e+000 2.9701028e-030 -5.9054457e+002 1.9980020e-002 1.0238257e-004 3.2621866e-002 4.2738365e-009 -1.6738364e+002 3.9960040e-002 4.0986708e-004 6.5296747e-002 1.7123646e-008 -1.5532808e+002 5.9940060e-002 9.2346767e-004 9.8078048e-002 3.8634755e-008 -1.4826044e+002 7.9920080e-002 1.6448870e-003 1.3101996e-001 6.8950813e-008 -1.4322921e+002 9.9900100e-002 2.5765350e-003 1.6417786e-001 1.0827599e-007 -1.3930936e+002 1.1988012e-001 3.7215561e-003 1.9760876e-001 1.5687814e-007 -1.3608875e+002 1.3986014e-001 5.0838652e-003 2.3137174e-001 2.1509300e-007 -1.3334747e+002 1.5984016e-001 6.6681924e-003 2.6552845e-001 2.8332961e-007 -1.3095416e+002
データはこのような形で保存しておくとあとで利用しやすい。
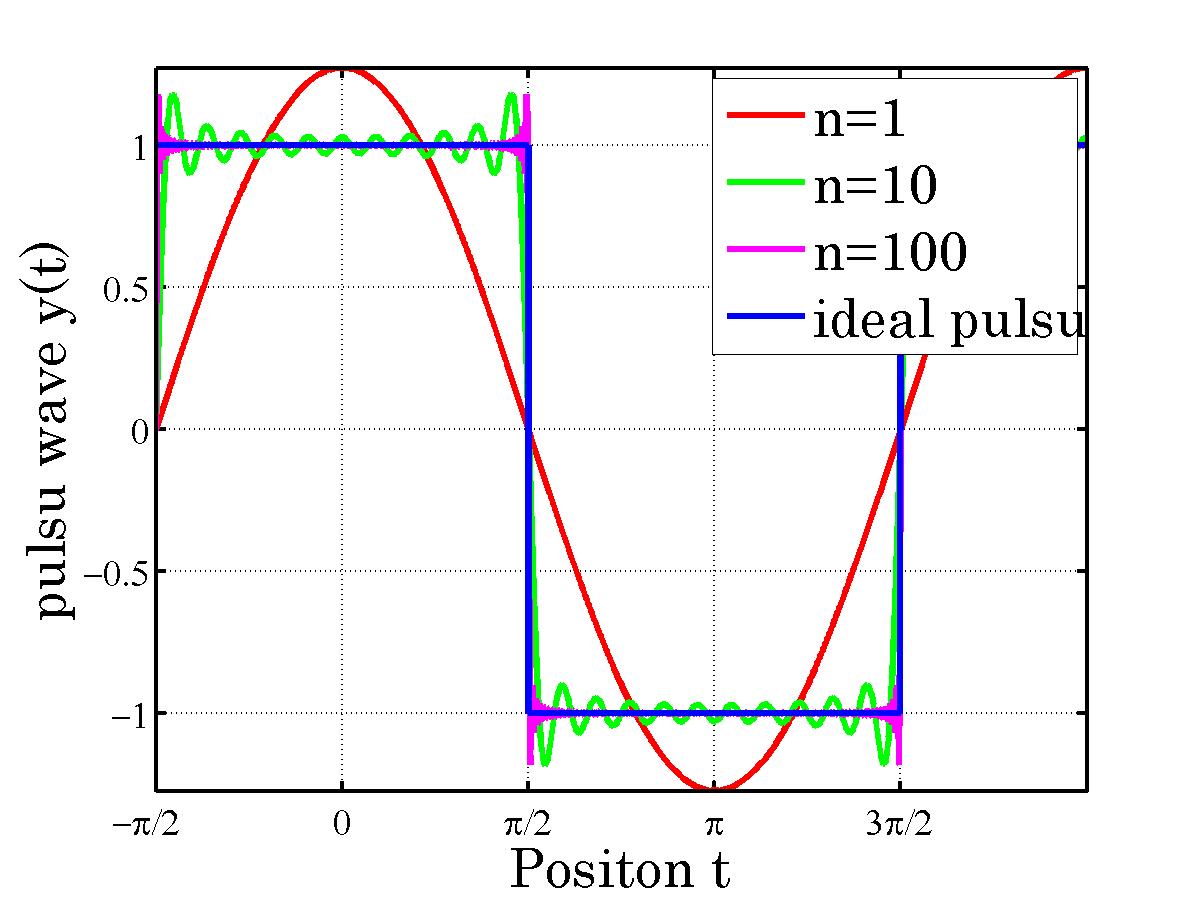
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% パルス波形を表示
% programming by embedded samurai
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
echo off
clear all
close all
%サンプリング周期 1[ms]
dx=1e-3;
% xの範囲は -pi/2から0.001単位で2piまで
x=[-pi/2:dx:2*pi];
xx = x/pi;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 注意!
% cos(n*x) n=omega
% n=omega=1,2,..,n である。
% omega = 2*pi*f = 1,2,...,n の意味なので
% 周波数的には、
% f= 1/2pi,2/2pi,3/2pi,...,n
% = 0.1592[Hz],0.3183[Hz],0.4775[Hz],0.6366[Hz],
% = 0.7958[Hz],0.9549[Hz],1.1141[Hz],....,n
%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 1[Hz]を表示
% ここはテスト
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
figure(1);
ty1=sin(2*pi*1*x);
%1[Hz]に近い
ty2=sin(6.2832*x);
plot(xx,ty1,'r-','linewidth',2);
hold on;
plot(xx,ty2,'b--','linewidth',3);
% xラベルとその文字の大きさ、線の太さの設定
str={'-p/2','0','p/2','p','3p/2','2p'}
set(gca,'FontName','symbol','xtick',[-0.5:.5:2],'xticklabel',str)
set(gca,'LineWidth',2,'FontSize',18)
% x-y範囲
axis([-Inf Inf -Inf Inf]);
grid on
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% n=1のとき
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
figure(2);
y1=0;
for m=0:1:0
y=(4/pi)*(1/(2*m+1))*(-1)^m*cos((2*m+1).*x);
y1=y1+y;
end
plot(xx,y1,'r-','linewidth',3);
hold on;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% n=10のとき
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
y2=0;
for m=0:1:10
y=(4/pi)*(1/(2*m+1))*(-1)^m*cos((2*m+1).*x);
y2=y2+y;
end
plot(xx,y2,'g-','linewidth',3);
hold on;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% n=100のとき
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
y3=0;
for m=0:1:100
y=(4/pi)*(1/(2*m+1))*(-1)^m*cos((2*m+1).*x);
y3=y3+y;
end
plot(xx,y3,'m-','linewidth',3);
hold on;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 理想パルス
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
data=[];
for n=x
if (n < pi/2)
y=1;
data=[data,y];
elseif (n >= pi/2) && (n <= 3*pi/2)
y=-1;
data=[data,y];
elseif ( n > 3*pi/2)
y=1;
data=[data,y];
end
end
plot(xx,data,'b-','linewidth',3);
hold on;
% xラベルとその文字の大きさ、線の太さの設定
str={'-p/2','0','p/2','p','3p/2','2p'}
set(gca,'FontName','symbol','xtick',[-0.5:.5:2],'xticklabel',str)
set(gca,'LineWidth',2,'FontSize',18)
% x-y範囲
axis([-Inf Inf -Inf Inf]);
grid on
% xラベル、yラベル
xlabel('Positon t','Fontsize',20,'FontName','Century');
ylabel('pulsu wave y(t)','Fontsize',20,'FontName','Century')
% キャプション
h=legend('n=1',...,
'n=10',...,
'n=100',...,
'ideal pulsu',...,
1);
set(h,'FontSize',20,'FontName','Century');
print -djpeg pulsuwave_t.jpeg
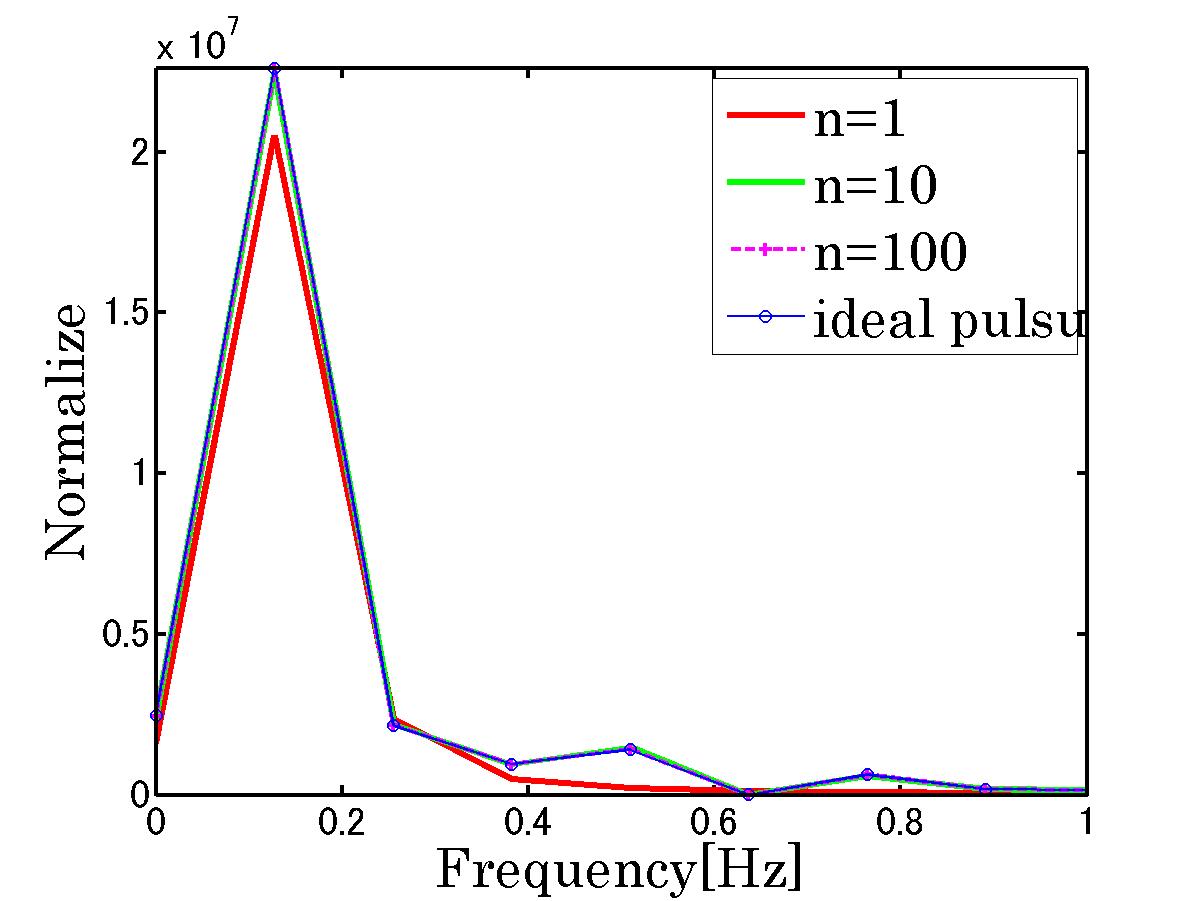
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
figure(3);
%サンプリング周波数 1kHz
df=1/dx
%xの数 7854
[gyo retu]=size(x)
%基本周波数 0.1273[Hz]
bf=df/retu
%FFTの結果は複素数である
fftdata1 = fft(y1)';
fftdata2 = fft(y2)';
fftdata3 = fft(y3)';
fftdata4 = fft(data)';
%FFTの絶対値を求める
power1=abs(fftdata1).^2;
power2=abs(fftdata2).^2;
power3=abs(fftdata3).^2;
power4=abs(fftdata4).^2;
%離散周波数を作る
freq = [0:retu-1]'*bf
plot(freq,power1,'r-','linewidth',3);
hold on
plot(freq,power2,'g-','linewidth',3);
hold on
plot(freq,power3,'m+--','linewidth',2);
hold on
plot(freq,power4,'bo-','linewidth',1);
hold on
axis([0 1 0 Inf]);
set(gca,'LineWidth',2,...,
'FontSize',15);
xlabel('Frequency[Hz]','Fontsize',20,'FontName','Century');
ylabel('Normalize','Fontsize',20,'FontName','Century');
% キャプション
h=legend('n=1',...,
'n=10',...,
'n=100',...,
'ideal pulsu',...,
1);
set(h,'FontSize',20,'FontName','Century');
print -djpeg pulsuwave_f.jpg
/***********************************************************/
/* FFT Test Program by embedded.samurai */
/* */
/***********************************************************/
#include <stdio.h>
#include <math.h>
#include "common.h"
#define INPUT_RECTANGLE 0
int main(void)
{
short i;
double wn_FFT[nFFT3_4]; //for twiddle factor
short br_FFT[nFFT]; //for bit reversal
double xr[nFFT],xi[nFFT];
double yr[nFFT],yi[nFFT];
double arg;
FILE *fin,*fout;
#if INPUT_RECTANGLE
//波形を作る
rectangle(xr,nFFT);
#else
fin = fopen("sin20hz.txt","r");
//入力データを配列に格納する
i=0;
while(1){
float buf;
fscanf(fin,"%f",&buf);
if(ferror(fin)){
printf("read error\n");
return(-1);
}
if(feof(fin)){
break;
}
xr[i++]= buf;
if(i>=nFFT){
fclose(fin);
break;
}
}//end of while(1)
#endif
//出力
fout = fopen("output_vc.txt","w");
//テーブルを作る generate tables for FFT
fft_table(wn_FFT,br_FFT,nFFT);
//出力データの配列を作る
for(i=0;i<nFFT;i++){
yr[i] = xr[i];
yi[i] = xi[i] = 0;
}
//FFTする
fft2(yr,yi,br_FFT,nFFT);
//FFT4に必要
//arg = 2*PI / nFFT;
//fft4(nFFT, arg, yr, yi);
//IFFTする
i_fft1(yr,yi,br_FFT,nFFT);
//結果を出力ファイルに格納する
for(i=0;i<nFFT;i++){
fprintf(fout,"%lf\t%lf\n",yr[i],yi[i]);
}
fclose(fout);
return 0;
}
/*============================================================*/
/* FFT programming by embedded.samurai */
/* */
/*============================================================*/
#include "common.h"
/***********************************************************************
* NAME : fft_table
* FUNCTION: FFTで使用するテーブルを作成する
* PROCESS : 省略
*
* INPUT : @param double wn_FFT[] -回転因子Wnのための配列
* : @param short br_FFT[] -ビット逆順のための配列
* : @param int N_FFT -FFTする全データ数
*
* OUTPUT : @param double wn_FFT[] -生成された回転因子Wnのための配列
* : @param short br_FFT[] -生成されたビット逆順のための配列
*
* RETURN : none
* CALL : none
/**********************************************************************/
void fft_table(double wn_FFT[],short br_FFT[],int N_FFT)
{
int i,n_half,ne,jp;
double arg;
int fft34=0;
//calculation of twiddle factor
arg = 2*PI / N_FFT;
fft34 = (N_FFT*3)/4;
for(i=0;i<fft34;i++){
wn_FFT[i] = (double)cos(arg*i);
#if DEBUG
printf("cos=%lf\tsin=%lf\n",cos(arg*i),sin(arg*i));
#endif
}
//calculation of bit reversal table
n_half = N_FFT/2;
br_FFT[0] = 0;
#if DEBUG
printf("br_FFT[%d]=0x%x\n",0,br_FFT[0]);
#endif
for(ne=1;ne<N_FFT;ne=ne<<1){
#if DEBUG
printf("ne=%d\n",ne);
#endif
for(jp=0;jp<ne;jp++){
br_FFT[jp+ne] = br_FFT[jp] + n_half;
#if DEBUG
printf("br_FFT[%d]=0x%x\n",jp+ne,br_FFT[jp+ne]);
#endif
}
n_half = n_half >> 1;
}
}//end of fft_table
/***************************************************************
* NAME : swap
* FUNCTION: データをひっくり返す
* PROCESS : 省略
* INPUT : @param double *a -データ
* : @param double *b -データ
*
* RETURN : none
* CALL : none
**************************************************************/
void swap(double *a,double *b){
double tmp;
tmp = *a;
*a = *b;
*b = tmp;
}
/***************************************************************
* NAME : fft1
* FUNCTION: テーブルを使ったFFT
* PROCESS : テーブルを使ったFFT 三上直樹氏のプログラム
*
* INPUT : @param double xR[] - FFTしたいデータ
* : @param short xI[] - FFTしたいデータ(全データ0を入れる)
* : @param double wn_FFT[] - 回転因子Wn配列
* : @param short br_FFT[] - ビット逆順配列
* : @param int N_FFT - FFTしたい全データ数(2の倍数)
*
* OUTPUT : @param double xR[] - FFTされたデータ
* : @param short xI[] - FFTされたデータ
*
* RETURN : none
* CALL : none
**************************************************************/
void fft1(double xR[],double xI[],double wn_FFT[],short br_FFT[],int N_FFT)
{
double xtmpR,xtmpI;
int j,jnh,k,jxC,jxS,ne,n_half,n_half2;
n_half = N_FFT / 2;
for(ne=1;ne<N_FFT;ne = ne<<1){
n_half2 = n_half *2;
#if DEBUG
printf("n_half2=%d\n",n_half2);
#endif
for(k=0;k<N_FFT;k=k+n_half2){
#if DEBUG
printf("k=%d\n",k);
#endif
jxC = 0;
jxS = N_FFT / 4;
for(j=k;j< (k+n_half);j++){
#if DEBUG
printf("j=%d\t",j);
#endif
jnh = j + n_half;
//beginning of butterfly operations
xtmpR = xR[j];
xtmpI = xI[j];
xR[j] = xtmpR + xR[jnh];
xI[j] = xtmpI + xI[jnh];
xtmpR = xtmpR - xR[jnh];
xtmpI = xtmpI - xI[jnh];
#if DEBUG
printf("jnh=%d,jxC=%d,jxS=%d\n",jnh,jxC,jxS);
#endif
xR[jnh] = xtmpR*wn_FFT[jxC] - xtmpI * wn_FFT[jxS];
xI[jnh] = xtmpR*wn_FFT[jxS] + xtmpI * wn_FFT[jxC];
//end of butterfly operations
jxC = jxC + ne;
jxS = jxS + ne;
}//end of for(j=k;j< (k+n_half);j++)
}//end of for(k=0;k<N_FFT;k=k+n_half2){
n_half = n_half >> 1;
}//end of for(ne=1;ne<N_FFT;ne = ne<<1)
//Bit reverse
//Bit reverse時のデータ取替えに注意
for(j=0;j<N_FFT;j++){
if(j<br_FFT[j]){
swap(&xR[j],&xR[br_FFT[j]]);
swap(&xI[j],&xI[br_FFT[j]]);
}
}
}
/***************************************************************
* NAME : fft2
* FUNCTION: テーブルを使用しないFFT
* PROCESS : 直接sin cosを計算する 三上直樹氏のプログラムを改良
*
* INPUT : @param double real[] - FFTしたいデータ
* : @param double imag[] - FFTしたいデータ(全データ0を入れる)
* : @param short bitreverse[] - ビット逆順配列
* : @param int fftNum - FFTしたい全データ数(2の倍数)
*
* OUTPUT : @param double real[] - FFTされたデータ
* : @param double imag[] - FFTされたデータ
*
* RETURN : none
* CALL : none
**************************************************************/
void fft2(double real[],double imag[],short bitreverse[],int fftNum)
{
double xtmpr,xtmpi;
int j,jnh,k,jxC,jxS,n_half,n_half2;
int step;
double arg;
n_half = fftNum / 2;
#if DEBUG
for(j=0;j<fftNum;j++){
printf("real[%d]=%lf\n",j,real[j]);
}
#endif
for(step=1;step < fftNum;step = step*2){
n_half2 = n_half *2;
#if DEBUG
printf("n_half2=%d\n",n_half2);
#endif
for(k=0;k<fftNum;k=k+n_half2){
#if DEBUG
printf("k=%d\n",k);
#endif
jxC = 0;
jxS = fftNum / 4;
for(j=k;j< (k+n_half);j++){
#if DEBUG
printf("j=%d\t",j);
#endif
//jに対してn_half分移動したところと両者を演算する
jnh = j + n_half;
xtmpr = real[j];
xtmpi = imag[j];
//バタフライ演算の上側には回転子の項がないため楽
real[j] = xtmpr + real[jnh];
imag[j] = xtmpi + imag[jnh];
//バタフライ演算の下の項には回転子の項があるため注意!!
xtmpr = xtmpr - real[jnh];
xtmpi = xtmpi - imag[jnh];
/*
(A+jB)*(cosx+jsinx)
Acosx + jAsinx +jBcosx-Bsinx
realpart-> Acosx - Bsinx
imagpart-> Asinx + Bcosx
*/
arg = 2*PI / fftNum;
//real[jnh] = xtmpr*cos(arg*jxC) - xtmpi * sin(arg*jxC);
//imag[jnh] = xtmpr*sin(arg*jxC) + xtmpi * cos(arg*jxC);
real[jnh] = xtmpr*cos(arg*jxC) + xtmpi * sin(arg*jxC);
imag[jnh] = xtmpi*cos(arg*jxC) - xtmpr * sin(arg*jxC);
printf("jnh=%d,jxC=%d,jxS=%d\n",jnh,jxC,jxS);
printf("jnh=%d,jxC=%d,jxS=%d\n",jnh,jxC,jxS);
//回転子は次の演算領域に入ると2倍ずつ増える
jxC = jxC + step;
jxS = jxS + step;
}
}
n_half = n_half / 2;
}
//Bit reverse
for(j=0;j<fftNum;j++){
//条件判定ない場合 ひっくり返したあとまたひっくり返すので注意!!
if(j<bitreverse[j]){
swap((double *)&real[j],(double *)&real[bitreverse[j]]);
swap((double *)&imag[j],(double *)&imag[bitreverse[j]]);
}
}
}
/************************************************************************
* NAME : fft4
* FUNCTION: 周波数間引きFFT programming by 大浦拓哉
* PROCESS : このプログラムは,"FFT (高速フーリエ・コサイン・サイン変換)
* の概略と設計法"のページ :
* http://www.kurims.kyoto-u.ac.jp/~ooura/fftman/
* のCソースです。
*
* INPUT : @param int n - FFTしたい全データ数(2の倍数)
* : @param double theta -
* : @param double ar[] - FFTしたいデータ
* : @param double ai[] - FFTしたいデータ(全データ0を入れる)
*
* OUTPUT : @param double ar[] - FFTされたデータ
* : @param double ai[] - FFTされたデータ
*
* RETURN : none
* CALL : none
*************************************************************************/
void fft4(int n, double theta, double ar[], double ai[])
{
int m, mh, i, j, k;
double wr, wi, xr, xi;
/* ---- scrambler ---- */
i = 0;
for (j = 1; j < n - 1; j++) {
for (k = n >> 1; k > (i ^= k); k >>= 1);
if (j < i) {
xr = ar[j];
xi = ai[j];
ar[j] = ar[i];
ai[j] = ai[i];
ar[i] = xr;
ai[i] = xi;
}
}
theta *= n;
#if DEBUG
printf("theta=%lf\n",theta);
#endif
for (mh = 1; (m = mh << 1) <= n; mh = m) {
#if DEBUG
printf("mh=%d\n",mh);
printf("m=%d\n",m);
#endif
theta *= 0.5;
#if DEBUG
printf("theta=%lf\n",theta);
#endif
for (i = 0; i < mh; i++) {
wr = cos(theta * i);
wi = sin(theta * i);
#if DEBUG
printf("theta*i=%lf\n",theta*i);
#endif
for (j = i; j < n; j += m) {
k = j + mh;
#if DEBUG
printf("j=%d\tk=%d\n",j,k);
#endif
xr = wr * ar[k] - wi * ai[k];
xi = wr * ai[k] + wi * ar[k];
ar[k] = ar[j] - xr;
ai[k] = ai[j] - xi;
ar[j] += xr;
ai[j] += xi;
}
}
}
}
/***************************************************************
* NAME : fft5
* FUNCTION: 時間間引きFFT
* PROCESS : 直接sin cosを計算する 三上直樹氏のプログラムを改良
*
* INPUT : @param double real[] - FFTしたいデータ
* : @param double imag[] - FFTしたいデータ(全データ0を入れる)
* : @param short bitreverse[] - ビット逆順配列
* : @param int fftNum - FFTしたい全データ数(2の倍数)
*
* OUTPUT : @param double real[] - FFTされたデータ
* : @param double imag[] - FFTされたデータ
*
* RETURN : none
* CALL : none
**************************************************************/
void fft5(double real[],double imag[],short bitreverse[],int fftNum)
{
double xtmpr,xtmpi;
int j,jnh,k,jxC,jxS,n_half,n_half2;
int step;
double arg;
for(j=0;j<fftNum;j++){
//条件判定ない場合 ひっくり返したあとまたひっくり返すので注意!!
if(j<bitreverse[j]){
swap(&real[j],&real[bitreverse[j]]);
swap(&imag[j],&imag[bitreverse[j]]);
}
}
n_half = 1;
n_half2 = 2;
for(step=fftNum/2;step >= 1 ;step = step/2){
for(k=0;k<fftNum;k=k+n_half2){
#if DEBUG
printf("k=%d\n",k);
#endif
jxC = 0;
jxS = fftNum / 4;
for(j=k;j< (k+n_half);j++){
#if DEBUG
printf("j=%d\t",j);
#endif
//jに対してn_half分移動したところと両者を演算する
jnh = j + n_half;
xtmpr = real[jnh];
xtmpi = imag[jnh];
arg = 2*PI / fftNum;
real[jnh] = xtmpr*cos(arg*jxC) + xtmpi * sin(arg*jxC);
imag[jnh] = xtmpi*cos(arg*jxC) - xtmpr * sin(arg*jxC);
#if DEBUG
printf("arg*jxC=%lf\n",arg*jxC);
#endif
xtmpr = real[j];
xtmpi = imag[j];
real[j] = xtmpr + real[jnh];
imag[j] = xtmpi + imag[jnh];
real[jnh] = xtmpr - real[jnh];
imag[jnh] = xtmpi - imag[jnh];
//回転子は次の演算領域に入ると1/2倍ずつ増える
jxC = jxC + step;
//jxS = jxS + step;
}
}
n_half = n_half * 2;
n_half2 = n_half2 * 2;
}
}
#include "common.h"
/***************************************************************
* NAME : i_fft1
* FUNCTION: 逆FFT
* PROCESS : 直接sin cosを計算する
*
* INPUT : @param double real[] - FFTされたデータ
* : @param double imag[] - FFTされたデータ
* : @param short bitreverse[] - ビット逆順配列
* : @param int fftNum - 逆FFTしたい全データ数(2の倍数)
*
* OUTPUT : @param double real[] - 逆FFTされたデータ
* : @param double imag[] - 逆FFTされたデータ
*
* RETURN : none
* CALL : none
**************************************************************/
void i_fft1(double real[],double imag[],short bitreverse[],int fftNum)
{
double xtmpr,xtmpi;
int j,jnh,k,jxC,jxS,n_half,n_half2;
int step;
double arg;
n_half = fftNum / 2;
#if DEBUG
for(j=0;j<fftNum;j++){
printf("real[%d]=%lf\n",j,real[j]);
}
#endif
for(step=1;step < fftNum;step = step*2){
n_half2 = n_half *2;
#if DEBUG
printf("n_half2=%d\n",n_half2);
#endif
for(k=0;k<fftNum;k=k+n_half2){
#if DEBUG
printf("k=%d\n",k);
#endif
jxC = 0;
jxS = fftNum / 4;
for(j=k;j< (k+n_half);j++){
#if DEBUG
printf("j=%d\t",j);
#endif
//jに対してn_half分移動したところと両者を演算する
jnh = j + n_half;
xtmpr = real[j];
xtmpi = imag[j];
//バタフライ演算の上側には回転子の項がないため楽
real[j] = xtmpr + real[jnh];
imag[j] = xtmpi + imag[jnh];
//バタフライ演算の下の項には回転子の項があるため注意!!
xtmpr = xtmpr - real[jnh];
xtmpi = xtmpi - imag[jnh];
/* (A+jB)*(cosx+jsinx)
Acosx + jAsinx +jBcosx-Bsinx
realpart-> Acosx - Bsinx
imagpart-> Asinx + Bcosx
*/
arg = 2*PI / fftNum;
real[jnh] = xtmpr*cos(arg*jxC) - xtmpi * sin(arg*jxC);
imag[jnh] = xtmpr*sin(arg*jxC) + xtmpi * cos(arg*jxC);
//real[jnh] = xtmpr*cos(arg*jxC) + xtmpi * sin(arg*jxC);
//imag[jnh] = xtmpi*cos(arg*jxC) - xtmpr * sin(arg*jxC);
#if DEBUG
printf("jnh=%d,jxC=%d,jxS=%d\n",jnh,jxC,jxS);
printf("jnh=%d,jxC=%d,jxS=%d\n",jnh,jxC,jxS);
#endif
//end of butterfly operations
//回転子は次の演算領域に入ると2倍ずつ増える
jxC = jxC + step;
jxS = jxS + step;
}
}
n_half = n_half / 2;
}
//Bit reverse
for(j=0;j<fftNum;j++){
//条件判定ない場合 ひっくり返したあとまたひっくり返すので注意!!
if(j<bitreverse[j]){
swap(&real[j],&real[bitreverse[j]]);
swap(&imag[j],&imag[bitreverse[j]]);
}
}
for(j=0;j<fftNum;j++){
real[j] = real[j] / fftNum;
imag[j] = imag[j] / fftNum;
}
}