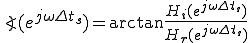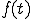 に対する次の定積分
に対する次の定積分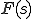 を
を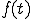 のラプラス変換という。
のラプラス変換という。
(1)「例題で学ぶ過渡現象」 大重力、森本義広、神田一伸 共著 森北出版
(2)「ディジタル信号処理技術」玉井徳みち、長島厚、藤田泰弘、若井修造著 日経BP社
(3)「ディジタル信号処理の基礎」三上直樹著 CQ出版
(4)「C言語によるディジタル信号処理入門」三上直樹著 CQ出版
(5)「アナログ&ディジタルフィルタ入門」小野浩司著 日刊工業
(6)「フーリエの冒険」ヒッポファミリークラブ
任意の時間関数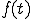 に対する次の定積分
に対する次の定積分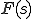 を
を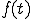 のラプラス変換という。
のラプラス変換という。
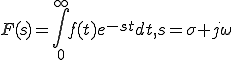
基本的に証明をして納得したあと、使用するときはラプラス変換-逆変換表を使用する
| No. | f(t) | F(s) | 備考 |
|---|---|---|---|
| 1 | 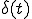 |
1 | |
| 2 | 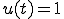 |
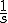 |
|
| 3 | 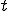 |
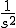 |
|
| 3 | 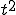 |
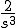 |
|
| 3 | 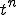 |
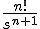 |
|
| 4 | 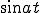 |
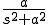 |
|
| 4 | 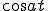 |
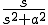 |
|
| 5 | 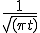 |
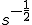 |
|
| 6 | 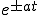 |
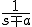 |
|
| 6 | 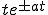 |
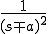 |
|
| 6 | 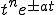 (nは正数) (nは正数) |
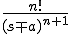 |
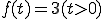 のラプラス変換
のラプラス変換
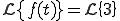
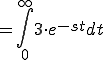
![= 3 [ -\frac{1}{s} \cdot e^{-st} ]^{\infty}_{0} = 3 [ -\frac{1}{s} \cdot e^{-st} ]^{\infty}_{0}](A5E9A5D7A5E9A5B9CAD1B4B9A4C85ACAD1B4B9_eq0029.gif)
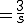
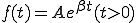 のラプラス変換
のラプラス変換
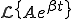
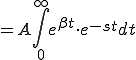
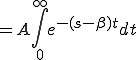
![= A [ -\frac{1}{(s-\beta)} \cdot e^{-(s-\beta)t} ]^{\infty}_{0} = A [ -\frac{1}{(s-\beta)} \cdot e^{-(s-\beta)t} ]^{\infty}_{0}](A5E9A5D7A5E9A5B9CAD1B4B9A4C85ACAD1B4B9_eq0035.gif)
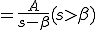
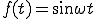 のラプラス変換
のラプラス変換部分積分法を使用する
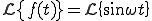
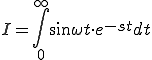
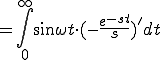
![= [ \sin \omega t \cdot (-\frac{e^{-st}}{s}) ]^{\infty}_{0} - \int_0^{\infty} \omega \cos \omega t \cdot (-\frac{e^{-st}}{s})dt = [ \sin \omega t \cdot (-\frac{e^{-st}}{s}) ]^{\infty}_{0} - \int_0^{\infty} \omega \cos \omega t \cdot (-\frac{e^{-st}}{s})dt](A5E9A5D7A5E9A5B9CAD1B4B9A4C85ACAD1B4B9_eq0041.gif)
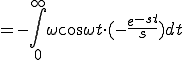

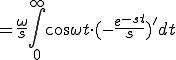
![= \frac{\omega}{s} [ \cos \omega t \cdot (-\frac{e^{-st}}{s}) ]^{\infty}_{0} - \int_0^{\infty} \omega \sin \omega t \cdot (-\frac{e^{-st}}{s})dt = \frac{\omega}{s} [ \cos \omega t \cdot (-\frac{e^{-st}}{s}) ]^{\infty}_{0} - \int_0^{\infty} \omega \sin \omega t \cdot (-\frac{e^{-st}}{s})dt](A5E9A5D7A5E9A5B9CAD1B4B9A4C85ACAD1B4B9_eq0045.gif)
ゆえに
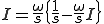
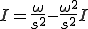
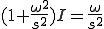
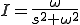
ゆえに
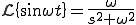
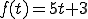 のラプラス変換
のラプラス変換部分積分法を使う
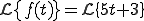
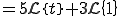
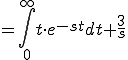
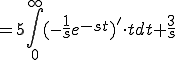
![= 5 \{ \[- \frac{1}{s}e^{-st} \cdot t \]^{\infty}_{0} - \int_0^{\infty} (-\frac{1}{s})e^{-st} dt \} + \frac{3}{s} = 5 \{ \[- \frac{1}{s}e^{-st} \cdot t \]^{\infty}_{0} - \int_0^{\infty} (-\frac{1}{s})e^{-st} dt \} + \frac{3}{s}](A5E9A5D7A5E9A5B9CAD1B4B9A4C85ACAD1B4B9_eq0056.gif)
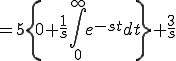
![=\frac{5}{s} \[ -\frac{1}{s} e^{-st} \]^{\infty}_{0} + \frac{3}{s} =\frac{5}{s} \[ -\frac{1}{s} e^{-st} \]^{\infty}_{0} + \frac{3}{s}](A5E9A5D7A5E9A5B9CAD1B4B9A4C85ACAD1B4B9_eq0058.gif)
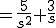
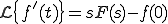
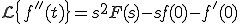
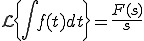
![\lim_{s \to 0}\[sF(s)\] = \lim_{t \to \infty}f(t) \lim_{s \to 0}\[sF(s)\] = \lim_{t \to \infty}f(t)](A5E9A5D7A5E9A5B9CAD1B4B9A4C85ACAD1B4B9_eq0063.gif)
基本的に変換表を見て行う
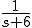
Ans.
変換表より
![{\cal L}^{-1} \[F(s)\] = {\cal L}^{-1} \[ \frac{1}{s+\alpha}\] = e^{-\alpha t} {\cal L}^{-1} \[F(s)\] = {\cal L}^{-1} \[ \frac{1}{s+\alpha}\] = e^{-\alpha t}](A5E9A5D7A5E9A5B9CAD1B4B9A4C85ACAD1B4B9_eq0065.gif)
ここで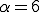 とすれば良いので
とすれば良いので![f(t) = {\cal L}^{-1} \[F(s)\] = e^{-6 t} f(t) = {\cal L}^{-1} \[F(s)\] = e^{-6 t}](A5E9A5D7A5E9A5B9CAD1B4B9A4C85ACAD1B4B9_eq0067.gif)
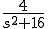
変換表より
![{\cal L}^{-1} \[ \frac{a}{s^2 + a^2}\] = \sin a t {\cal L}^{-1} \[ \frac{a}{s^2 + a^2}\] = \sin a t](A5E9A5D7A5E9A5B9CAD1B4B9A4C85ACAD1B4B9_eq0069.gif)
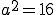 より
より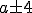 よって
よって
![{\cal L}^{-1} \[ \frac{\pm 4}{s^2 + (\pm4)^2}\] = \sin( \pm 4 t) {\cal L}^{-1} \[ \frac{\pm 4}{s^2 + (\pm4)^2}\] = \sin( \pm 4 t)](A5E9A5D7A5E9A5B9CAD1B4B9A4C85ACAD1B4B9_eq0072.gif)
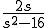
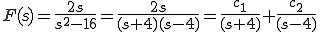
とおく。
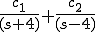
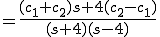
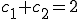
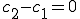
ゆえに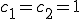
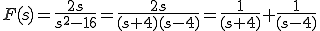
![{\cal L}^{-1} \[ F(s) \] = f(t) = e^{-4t} + e^{4t} {\cal L}^{-1} \[ F(s) \] = f(t) = e^{-4t} + e^{4t}](A5E9A5D7A5E9A5B9CAD1B4B9A4C85ACAD1B4B9_eq0081.gif)
注意! 信号は直流である
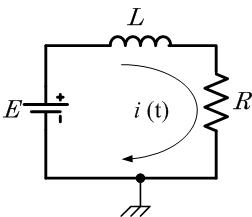
直流電圧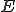 を印加したときの、回路に流れる電流
を印加したときの、回路に流れる電流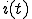 をもとめる。
をもとめる。
Ans.
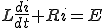
ここで
![{\cal L}\[ \frac{di}{dt} \] = s I(s) - i(0) {\cal L}\[ \frac{di}{dt} \] = s I(s) - i(0)](A5E9A5D7A5E9A5B9CAD1B4B9A4C85ACAD1B4B9_eq0085.gif)
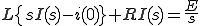
いま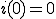 (初期条件)とすると
(初期条件)とすると
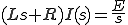
ゆえに
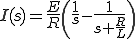
この式をラプラス逆変換すると
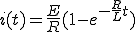
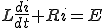 (1)
(1)
この微分方程式の一般解は、
特解(定常解) 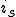
と
式(1)で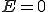 とおいた場合の一般解(過渡解)
とおいた場合の一般解(過渡解)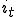 の和で表される。
の和で表される。
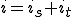
定常解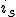 を以下のようにしてもとめる。
を以下のようにしてもとめる。
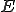 は定数であるため、
は定数であるため、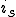 は定数となる。
は定数となる。
そのため時間変化がないから 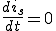 となるため(1)は、
となるため(1)は、
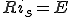
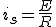
次に過渡解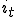 は、
は、
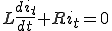
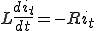
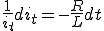
両辺を積分すると
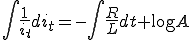
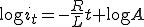
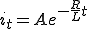
よって一般解は、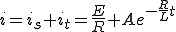
初期条件は、t=0のとき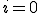 なので、
なので、
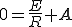
ゆえに
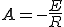
つまり
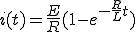
この式は時間の経過とともに過度状態が終わり電流は、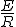 に収束することを示している。
に収束することを示している。
Z変換は基本的にラプラス変換と同じである。
両者の変数は、次の関係
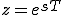
で結ばれる。
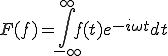 (3-1)
(3-1)
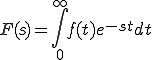 (3-2)
(3-2)
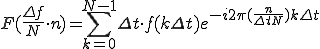
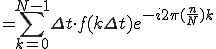 (3-3)
(3-3)
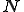 ::取得するデータの総数
::取得するデータの総数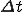 ::サンプリング周期
::サンプリング周期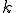 ::何番目の値か?
::何番目の値か?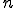 ::基本周波数の何倍か?
::基本周波数の何倍か?
サンプリング周波数 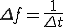
基本周波数 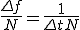
![X(z) = \sum_{n=0}^{\infty} x[n] z^{-n} X(z) = \sum_{n=0}^{\infty} x[n] z^{-n}](A5E9A5D7A5E9A5B9CAD1B4B9A4C85ACAD1B4B9_eq0126.gif) (3-4)
(3-4)
ここで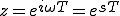 ここで
ここで 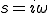
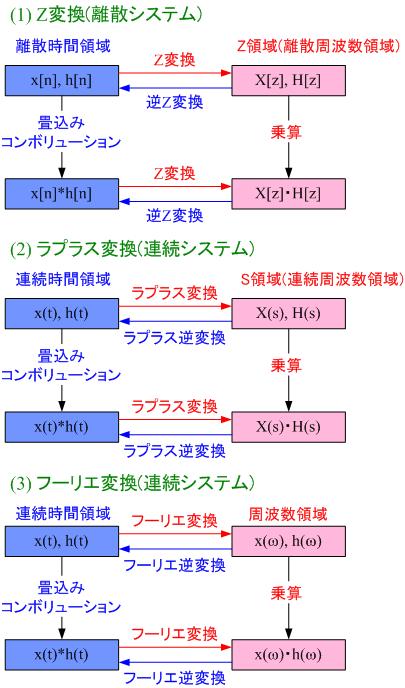
(1)連続の世界での畳込み
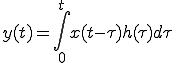
をラプラス変換すると
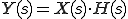
(2)離散の世界での畳込み
![y[n] = \sum_{k=0}^{n} x[n-k] \cdot h[k] y[n] = \sum_{k=0}^{n} x[n-k] \cdot h[k]](A5E9A5D7A5E9A5B9CAD1B4B9A4C85ACAD1B4B9_eq0131.gif)
をZ変換すると
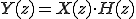
ディジタルフィルタでのz変換の使用目的は、
(1) 畳み込み![y[n]= \sum_{k=0}^{N-1} (h[k] x[n-k]) y[n]= \sum_{k=0}^{N-1} (h[k] x[n-k])](A5E9A5D7A5E9A5B9CAD1B4B9A4C85ACAD1B4B9_eq0133.gif)
の簡略化
(2) 周波数特性の導出
がある。
ディジタル信号を![x[n] x[n]](A5E9A5D7A5E9A5B9CAD1B4B9A4C85ACAD1B4B9_eq0134.gif) ,その個数を
,その個数を 個とすれば、
個とすれば、![x[n] x[n]](A5E9A5D7A5E9A5B9CAD1B4B9A4C85ACAD1B4B9_eq0136.gif) のz変換は、
のz変換は、
![X[z] = \sum_{n=0}^{N-1} x[n]z^{-n} X[z] = \sum_{n=0}^{N-1} x[n]z^{-n}](A5E9A5D7A5E9A5B9CAD1B4B9A4C85ACAD1B4B9_eq0137.gif) (1)
(1)
によって定義される。
いま、インパルス信号
![x[n] = \delta[n] + \delta[n-1] x[n] = \delta[n] + \delta[n-1]](A5E9A5D7A5E9A5B9CAD1B4B9A4C85ACAD1B4B9_eq0138.gif)
![x[0]=1,x[1]=1 x[0]=1,x[1]=1](A5E9A5D7A5E9A5B9CAD1B4B9A4C85ACAD1B4B9_eq0139.gif)
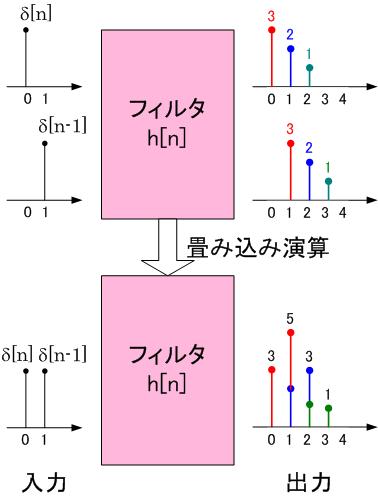
フィルタ係数は、
![h[0]=3, h[1]=2, h[2]=1 h[0]=3, h[1]=2, h[2]=1](A5E9A5D7A5E9A5B9CAD1B4B9A4C85ACAD1B4B9_eq0140.gif)
![h[n] = 3\delta[n]+2\delta[n-1]+\delta[n-2] h[n] = 3\delta[n]+2\delta[n-1]+\delta[n-2]](A5E9A5D7A5E9A5B9CAD1B4B9A4C85ACAD1B4B9_eq0141.gif)
たたみこみをまとめると
![y[n] = \sum_{k=0}^{2} (h[k] x[n-k]) y[n] = \sum_{k=0}^{2} (h[k] x[n-k])](A5E9A5D7A5E9A5B9CAD1B4B9A4C85ACAD1B4B9_eq0142.gif)
![=h[0]x[n-0] + h[1]x[n-1] + h[2]x[n-2] =h[0]x[n-0] + h[1]x[n-1] + h[2]x[n-2]](A5E9A5D7A5E9A5B9CAD1B4B9A4C85ACAD1B4B9_eq0143.gif)
![=3x[n-0] + 2x[n-1] + x[n-2] =3x[n-0] + 2x[n-1] + x[n-2]](A5E9A5D7A5E9A5B9CAD1B4B9A4C85ACAD1B4B9_eq0144.gif)
![y[0]=3x[0] + 2x[-1] + x[-2] = 3 y[0]=3x[0] + 2x[-1] + x[-2] = 3](A5E9A5D7A5E9A5B9CAD1B4B9A4C85ACAD1B4B9_eq0145.gif)
![y[1]=3x[1] + 2x[0] = 5 y[1]=3x[1] + 2x[0] = 5](A5E9A5D7A5E9A5B9CAD1B4B9A4C85ACAD1B4B9_eq0146.gif)
![y[2]=2x[1] + x[0] = 3 y[2]=2x[1] + x[0] = 3](A5E9A5D7A5E9A5B9CAD1B4B9A4C85ACAD1B4B9_eq0147.gif)
![y[3]= x[1] = 1 y[3]= x[1] = 1](A5E9A5D7A5E9A5B9CAD1B4B9A4C85ACAD1B4B9_eq0148.gif)
![y[4]= 0 y[4]= 0](A5E9A5D7A5E9A5B9CAD1B4B9A4C85ACAD1B4B9_eq0149.gif)
という計算をしていく必要がある。入力はたった2入力だが、計算は4出力である。
まず入力x[n]をZ変換する。
![X(z) = \sum_{n=0}^{N-1} x[n]z^{-n} X(z) = \sum_{n=0}^{N-1} x[n]z^{-n}](A5E9A5D7A5E9A5B9CAD1B4B9A4C85ACAD1B4B9_eq0150.gif)
信号は2入力なので、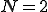 である。
である。
![X(z) = \sum_{n=0}^{1} x[n]z^{-n} X(z) = \sum_{n=0}^{1} x[n]z^{-n}](A5E9A5D7A5E9A5B9CAD1B4B9A4C85ACAD1B4B9_eq0152.gif)
![= x[0]z^{-0} + x[1]z^{-1} = x[0]z^{-0} + x[1]z^{-1}](A5E9A5D7A5E9A5B9CAD1B4B9A4C85ACAD1B4B9_eq0153.gif)
![= x[0] + x[1]z^{-1} = x[0] + x[1]z^{-1}](A5E9A5D7A5E9A5B9CAD1B4B9A4C85ACAD1B4B9_eq0154.gif)
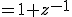
次にh[n]をZ変換する。
![H(z) = \sum_{n=0}^{2} h[n]z^{-n} H(z) = \sum_{n=0}^{2} h[n]z^{-n}](A5E9A5D7A5E9A5B9CAD1B4B9A4C85ACAD1B4B9_eq0156.gif)
![= h[0]z^{-0} + h[1]z^{-1} +h[2]z^{-2} = h[0]z^{-0} + h[1]z^{-1} +h[2]z^{-2}](A5E9A5D7A5E9A5B9CAD1B4B9A4C85ACAD1B4B9_eq0157.gif)
![= h[0] + h[1]z^{-1} +h[2]z^{-2} = h[0] + h[1]z^{-1} +h[2]z^{-2}](A5E9A5D7A5E9A5B9CAD1B4B9A4C85ACAD1B4B9_eq0158.gif)
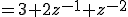
次に畳み込みのZ変換は、
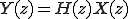
つまり、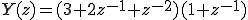
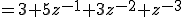
これを逆Z変換すると
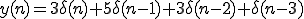
ゆえに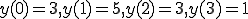
このようにz変換を使うと畳み込みが単純な積となり簡単に計算できる。
これがz変換を使う第一の理由である。
ディジタルフィルタでの周波数特性は、
フィルタ係数h(n)を、z変換して求めます。
h(n)のz変換H(z)に対してzを、
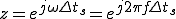
(ここで 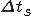 はサンプリング周期)
はサンプリング周期)
と置き換えた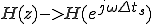
が周波数特性となる。
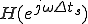 は複素数なので
は複素数なので
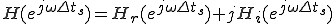
と表せます。
そしてフィルタの振幅特性と位相特性は、
振幅特性: 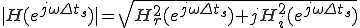
位相特性: